题目内容
4.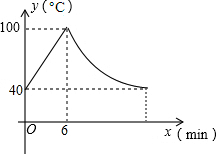 某型号的饮水机接通电源后就进入自动加热程序,水温升至100℃后自动停止加热,停止加热后水温开始下降,当水温降至40℃,饮水机再次启动自动加热,重复上述程序,一个周期内水温y(℃)与时间t(min)的关系如图所示,(水温上升过程中温度与时间成一次函数;水温下降过程中,温度与时间成反比例函数),根据图象,解答下列问题:
某型号的饮水机接通电源后就进入自动加热程序,水温升至100℃后自动停止加热,停止加热后水温开始下降,当水温降至40℃,饮水机再次启动自动加热,重复上述程序,一个周期内水温y(℃)与时间t(min)的关系如图所示,(水温上升过程中温度与时间成一次函数;水温下降过程中,温度与时间成反比例函数),根据图象,解答下列问题:(1)饮水机工作一个周期的时间为多少分钟?
(2)一个周期内水温不低于50°的时间为多少分钟?
分析 (1)首先求得反比例函数的解析式,然后代入y=40后求得时间即可得到答案;
(2)代入两个函数y=50求得两个时间相减即可确定答案.
解答 解:(1)设反比例函数关系式为:y=$\frac{k}{x}$,
将(6,100)代入,得k=600,
∴y=$\frac{600}{x}$,
将y=40代入y=$\frac{600}{x}$,解得:x=15;
∴饮水机接通电源到下一次开机的间隔时间为15分钟;
(2)设一次函数关系式为:y=k1x+b,
将(0,40),(6,100)代入y=k1x+b,
$\left\{\begin{array}{l}{b=40}\\{6{k}_{1}+b=100}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=10}\\{b=40}\end{array}\right.$,
∴y=10x+40(0≤x≤6),
将y=50代入y=$\frac{600}{x}$,
解得:x=12,
50=10x+40,
解得:x=1,
则12-1=11(min),
故要想喝到超过50℃的水,有11分钟.
点评 本题考查了反比例函数的应用,解题的关键是求得两个函数的解析式.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
19.若a+b=-6,ab=6,则$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$的值为( )
| A. | $\sqrt{6}$ | B. | -$\sqrt{6}$ | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
11.若关于x的不等式组$\left\{\begin{array}{l}{x-a>2}\\{b-2x>0}\end{array}\right.$的解集为-1<x<1,则(a+b)2017的值是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | -1 | D. | -$\frac{1}{2}$ |
12.考察反比例函数y=-$\frac{6}{x}$,下列结论中不正确的是( )
| A. | 图象必经过(-3,2) | B. | 当x>0时,y随x的增大而增大 | ||
| C. | 图象在第二、四象限内 | D. | 图象与直线y=x有两个交点 |
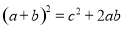 ,则这个三角形是( )
,则这个三角形是( ) 如图,有一张直角三角形纸片,两直角边AC=7cm,BC=11cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为$\frac{36}{11}$cm.
如图,有一张直角三角形纸片,两直角边AC=7cm,BC=11cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为$\frac{36}{11}$cm.