题目内容
15.观察下列数据:$\frac{2}{3}$,$-\frac{3}{9}$,$\frac{4}{27}$,$-\frac{5}{81}$…则第n个数为(-1)n+1$\frac{n+1}{{3}^{n}}$.分析 根据已知发现规律,奇数项为正,偶数项为负,分母为3n,分子为n+1,由此可得结果.
解答 解:∵奇数项为正,偶数项为负,分母为3n,分子为n+1,
∴第n个数为(-1)n+1$\frac{n+1}{{3}^{n}}$,
故答案为:(-1)n+1$\frac{n+1}{{3}^{n}}$.
点评 本题主要考查了数字的变化规律,根据已知发现每项符号,分子,分母的变化规律是解答此题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
5.观察下列图形:按照这样的规律,第n个图形有( )个★.


| A. | 3n-1 | B. | 3n+1 | C. | 3n+4 | D. | 4n+3 |
20.下列命题中是真命题的是( )
| A. | $\sqrt{9}$是无理数 | B. | 相等的角是对顶角 | ||
| C. | $\sqrt{\frac{1}{4}}=\frac{1}{2}$ | D. | -27没有立方根 |
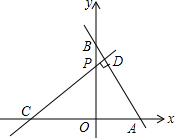 如图.在平面直角坐标系中,点C、点A为x轴上两点,OA、OC的长是方程y=x2-7x+12=0的两个根(OC>OA).点B在y轴上,CD⊥AB交y轴于点P,且CP=AB.
如图.在平面直角坐标系中,点C、点A为x轴上两点,OA、OC的长是方程y=x2-7x+12=0的两个根(OC>OA).点B在y轴上,CD⊥AB交y轴于点P,且CP=AB.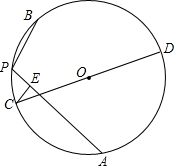 如图,PA、PB是⊙O的一条折弦,C是AB弧的中点,CD是⊙O的直径,CE⊥PA于E,求证:PD2-AD2=PA•PB.
如图,PA、PB是⊙O的一条折弦,C是AB弧的中点,CD是⊙O的直径,CE⊥PA于E,求证:PD2-AD2=PA•PB. 如图是一个圆台及其主视图,你能把它的俯视图和左视图补上吗?
如图是一个圆台及其主视图,你能把它的俯视图和左视图补上吗?