题目内容
6.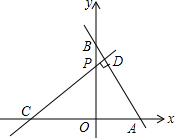 如图.在平面直角坐标系中,点C、点A为x轴上两点,OA、OC的长是方程y=x2-7x+12=0的两个根(OC>OA).点B在y轴上,CD⊥AB交y轴于点P,且CP=AB.
如图.在平面直角坐标系中,点C、点A为x轴上两点,OA、OC的长是方程y=x2-7x+12=0的两个根(OC>OA).点B在y轴上,CD⊥AB交y轴于点P,且CP=AB.(1)求点A、C的坐标.
(2)求直线CD的函数解析式.
(3)直线CD上是否存在点E,使△ACE为等腰三角形?若存在,请直接写出点E坐标;若不存在.请说明理由.
分析 (1)解方程x2-7x+12=0得OC=4,OA=3,即可得到结论;
(2)根据已知条件易求△PCO≌△ABO,于是得到OP=OA=3,OB=OC=4,求得p的坐标,再根据待定系数法可求得结论;
(3)易求AC=3-(-4)=7,分三种情况:①EC=EA,根据等腰三角形的性质可求得结论,②EC=CA=7,根据相似三角形的性质可求得结论,③EA=CA=7,有勾股定理求出结论.
解答 (1)解:解方程x2-7x+12=0得x1=3,x2=4,
∴OC=4,OA=3,
∴A(3,0),C(-4,0);
(2)∵CD⊥AB,x轴⊥y轴,
∴∠PCO=∠ABO=90°-∠BAO,
在△PCO和△ABO中,
$\left\{\begin{array}{l}{∠POC=∠AOB}\\{∠PCO=∠ABO}\\{CP=AB}\end{array}\right.$,
∴△PCO≌△ABO,
∴OP=OA=3,OB=OC=4,
∴P(0,3),
设直线AD解析式为y=kx+b,把P(0,3),C(-4,0)代入可得$\left\{\begin{array}{l}{b=3}\\{-4k+b=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{b=3}\\{k=\frac{3}{4}}\end{array}\right.$.
故直线CD的函数解析式为y=$\frac{3}{4}x+3$;
(3)AC=3-(-4)=7,CP=$\sqrt{{4}^{2}+{3}^{2}}$=5,
当EC=EA时,根据等腰三角形的性质,E点的横坐标为-$\frac{1}{2}$,
把x=-$\frac{1}{2}$代入y=$\frac{3}{4}x+3$得:y=$\frac{21}{8}$,即E(-$\frac{1}{2}$,$\frac{21}{8}$)
当EC=AC=7时,
设p(b,m),
∴$\frac{m}{PO}=\frac{EC}{PC}$,即$\frac{m}{3}=\frac{7}{5}$,
解得:m=$\frac{21}{5}$,
把y=$\frac{21}{5}$代入y=$\frac{3}{4}x+3$得x=$\frac{8}{5}$,即E($\frac{8}{5}$,$\frac{21}{5}$)
当EA=AC=7时,设E(n,$\frac{3}{4}n+3$),
由勾股定理得:(n-3)2+($\frac{3}{4}n+3$)2=AE2=72,
解得:n=$\frac{24}{50}$±$\frac{224}{50}$,
∵AP=$\sqrt{{3}^{2}+{3}^{2}}$=$\sqrt{18}$<7,
∴E在第一象限,
∴n>0,
∴n=$\frac{124}{25}$,n=4,
$\frac{3}{4}n+3$=$\frac{168}{25}$,
∴E($\frac{124}{25}$,$\frac{168}{25}$),(-$\frac{48}{5}$,-$\frac{21}{5}$),
综上所述:E的坐标为:E(-$\frac{48}{5}$,-$\frac{21}{5}$),E(-$\frac{1}{2}$,$\frac{21}{8}$),E($\frac{8}{5}$,$\frac{21}{5}$),E($\frac{124}{25}$,$\frac{168}{25}$).
点评 本题主要考查了一元二次方程,全等三角形的判定与性质,一次函数的解析式的求法,等腰三角形的性质,综合性强,能正确分类是解决问题的关键.

 如图,在平面直角坐标系中,A(0,1),B(-3,5),C(-3,1).
如图,在平面直角坐标系中,A(0,1),B(-3,5),C(-3,1).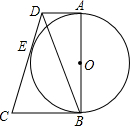 以AB为直径的⊙O分别与四边形ABCD的边切于点A、E、B,DB=DC.
以AB为直径的⊙O分别与四边形ABCD的边切于点A、E、B,DB=DC.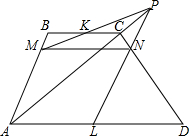 如图,在梯形ABCD的对角线AC的延长线上任取一点P,过点P与梯形两条底边的中点的连线分别交腰AB、CD于点M、N,求证:MN∥AD∥BC.
如图,在梯形ABCD的对角线AC的延长线上任取一点P,过点P与梯形两条底边的中点的连线分别交腰AB、CD于点M、N,求证:MN∥AD∥BC.