题目内容
3.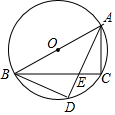 已知:如图,AB是⊙O的直径,AD平分∠BAC,BC=8,AC=6.求
已知:如图,AB是⊙O的直径,AD平分∠BAC,BC=8,AC=6.求(1)⊙O的半径;
(2)DB的长.
分析 (1)先根据圆周角定理求出∠C的度数,再由勾股定理求出AB的长,进而可得出结论;
(2)连接OD,根据等腰三角形的性质得出∠OAD=∠ODA,再由AD平分∠BAC可知∠OAD=∠CAD,故可得出∠BOD=∠OAC,所以OD∥AC,由三角形中位线定理得出OM是△ABC的平分线,故可得出OM的长,由相似三角形的判定得出△AEC∽△DEM,故可得出ME的长,进而得出BE的长,由△ACE∽△BDE即可得出DB的长.
解答 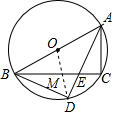 解:(1)∵AB是⊙O的直径,
解:(1)∵AB是⊙O的直径,
∴∠C=90°.
∵BC=8,AC=6,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∴OA=OB=5;
(2)连接OD,
∵OB=OD,
∴∠OAD=∠ODA.
∵AD平分∠BAC,
∴∠OAD=∠CAD,
∴∠BOD=∠OAC,
∴OD∥AC.
∵点O是线段AB的中点,
∴OM是△ABC的平分线,
∴OM=$\frac{1}{2}$AC=3,CM=BM=$\frac{1}{2}$BC=4.
∴DM=5-3=2.
∵∠AEC=∠DEM,∠CAE=∠MDE,
∴△AEC∽△DEM,
∴$\frac{AC}{DM}$=$\frac{CE}{ME}$,即$\frac{6}{2}$=$\frac{CE}{4-CE}$,解得CE=3,
∴ME=4-3=1,
∴BE=BM+ME=4+1=5.
∵∠AEC=∠BED,∠BDE=∠C=90°,
∴△ACE∽△BDE,
∴$\frac{AC}{BD}$=$\frac{CE}{BE}$,即$\frac{6}{BD}$=$\frac{3}{5}$,解得BD=10.
点评 本题考查的是圆周角定理,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
11.下列各图中的角,其中为圆周角的是( )
| A. |  | B. |  | C. |  | D. |  |
12.若t是一元二次方程ax2+bx+c=0(a≠0)的根,则判别式b2-4ac和完全平方式M=(2at+b)2的关系是( )
| A. | b2-4ac=M | B. | b2-4ac>M | ||
| C. | b2-4ac<M | D. | 大小关系不能确定 |
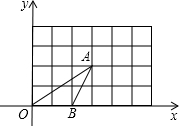 如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.
如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F. 已知有理数a、b在数轴上的位置如图,则比较a、b、-a、-b的大小为a<-b<b<-a.
已知有理数a、b在数轴上的位置如图,则比较a、b、-a、-b的大小为a<-b<b<-a. 已知,如图:∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF:
已知,如图:∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF: 如图一根木棒放在数轴上,数轴的1个单位长度为1cm,木棒的左端与数轴上的点A重合,右端与点B重合.
如图一根木棒放在数轴上,数轴的1个单位长度为1cm,木棒的左端与数轴上的点A重合,右端与点B重合.