题目内容
15.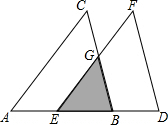 如图,把△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{4}{9}$,若AB=2,求△ABC移动的距离BE的长.
如图,把△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{4}{9}$,若AB=2,求△ABC移动的距离BE的长.
分析 根据平移的性质得到EF∥AC,证得△BEG∽△BAC,由相似三角形的性质得到$\frac{BE}{AB}$=$\sqrt{\frac{{S}_{△BEG}}{{S}_{△ABC}}}$=$\frac{2}{3}$,即可得到结论.
解答  解:∵把△ABC沿边BA平移到△DEF的位置,
解:∵把△ABC沿边BA平移到△DEF的位置,
∴EF∥AC,
∴△BEG∽△BAC,
∴$\frac{BE}{AB}$=$\sqrt{\frac{{S}_{△BEG}}{{S}_{△ABC}}}$=$\frac{2}{3}$,
∵AB=2,
∴BE=$\frac{4}{3}$.
点评 本题主要考查相似三角形的判定和性质、平移的性质,关键在于求证△ABC与阴影部分为相似三角形.

练习册系列答案
相关题目
5.下列各组中的两项,不是同类项的是( )
| A. | 2x2y与-2x2y | B. | x3与3x | C. | -3ab2c3与c3b2a | D. | 1与-8 |
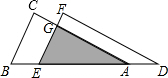 如图,△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{1}{9}$,若AB=2,求△ABC移动的距离BE的长.
如图,△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{1}{9}$,若AB=2,求△ABC移动的距离BE的长.