题目内容
4.计算:(1)3-3=$\frac{1}{27}$ (2)($\frac{1}{2}$)-3=8 (3)(-2)-2=$\frac{1}{4}$ (4)(-2)-5=-$\frac{1}{32}$
(5)(-a)-4=$\frac{1}{{a}^{4}}$ (6)(-a)-5=-$\frac{1}{{a}^{5}}$ (7)5-3=$\frac{1}{125}$ (8)2-2=$\frac{1}{4}$
(9)(2x)-2=$\frac{1}{4{x}^{2}}$.
分析 根据负整数指数次幂的性质,a-n=$\frac{1}{{a}^{n}}$(a≠0)即可求解.
解答 解:1)3-3=$\frac{1}{{3}^{3}}$=$\frac{1}{27}$;
(2)($\frac{1}{2}$)-3=23=8;
(3)(-2)-2=$\frac{1}{(-2)^{2}}$=$\frac{1}{4}$;
(4)(-2)-5=$\frac{1}{(-2)^{5}}$=-$\frac{1}{32}$;
(5)(-a)-4=$\frac{1}{(-a)^{4}}$=$\frac{1}{{a}^{4}}$;
(6)(-a)-5=$\frac{1}{(-a)^{5}}$=-$\frac{1}{{a}^{5}}$;
(7)5-3=$\frac{1}{{5}^{3}}$=$\frac{1}{125}$;
(8)2-2=$\frac{1}{{2}^{2}}$=$\frac{1}{4}$;
(9)(2x)-2=$\frac{1}{(2x)^{2}}$=$\frac{1}{4{x}^{2}}$.
故答案是:$\frac{1}{27}$,8,$\frac{1}{4}$,-$\frac{1}{32}$,$\frac{1}{{a}^{4}}$,-$\frac{1}{{a}^{5}}$,$\frac{1}{125}$,$\frac{1}{4}$,$\frac{1}{4{x}^{2}}$.
点评 本题主要考查了零指数幂,负整数指数幂的运算.负整数指数为正整数指数的倒数;任何非0数的0次幂等于1.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
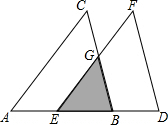 如图,把△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{4}{9}$,若AB=2,求△ABC移动的距离BE的长.
如图,把△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{4}{9}$,若AB=2,求△ABC移动的距离BE的长.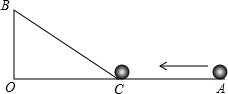 如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?