题目内容
17.端午节前夕,某校为学生购买了A、B两种品牌的粽子共400个,已知B品牌粽子的单价比A品牌粽子的单价的2倍少6元.(1)当买A品牌100个,B品牌粽子300个时,学校所花费用为4500元.求A、B两种品牌粽子各自的单价;
(2)在两种品牌粽子单价不变的情况下,由于资金临时出现状况,所花费用不超过4000元,问至少买A品牌粽子多少个?
分析 (1)设A品牌粽子的单价为x元,B品牌粽子的单价为y元.等量关系:B品牌粽子的单价=2×A品牌粽子的单价-6.100×A品牌数量,300×B品牌粽数量=4500;据此列出方程组,并解答;
(2)设买A品牌粽子a个,则买B品牌粽子(400-a)个.依据“所花费用不超过4000元”列出不等式.
解答 解:(1)设A品牌粽子的单价为x元,B品牌粽子的单价为y元.
根据题意得:$\left\{\begin{array}{l}y=2x-6\\ 100x+300y=4500\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=9\\ y=12\end{array}\right.$,
答:A品牌粽子的单价为9元,B品牌粽子的单价为12元.
(2)设买A品牌粽子a个,则买B品牌粽子(400-a)个.
根据题意得:9a+12(400-a)≤4000.
解得:$a≥266\frac{2}{3}$,满足题意的最小整数解为267.
答:至少买A品牌粽子267个.
点评 此题主要考查了一元一次不等式和二元一次方程组的应用,关键是弄清题意,根据关键语句算出A品牌粽子和B品牌粽子的单价.

练习册系列答案
相关题目
2.某商场经营一批进价为2元一件的小商品,在销售中发现此商品的日销售单价x(元)与日销售量y(件)之间有如下的一次函数关系:
(1)求y与x的函数解析式;
(2)求日销售额P(元)的最大值.
| x | 3 | 5 | 7 | … |
| y | 18 | 14 | 10 | … |
(2)求日销售额P(元)的最大值.
7.若直线y=3x+6与坐标轴围成的三角形面积为S,则S=( )
| A. | 3 | B. | 4 | C. | 6 | D. | 12 |
 △ABC中,AB=AC,∠BAC=120°,AD⊥BC,且AB=6cm,求AD的长.
△ABC中,AB=AC,∠BAC=120°,AD⊥BC,且AB=6cm,求AD的长. 如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为10$\sqrt{5}$.
如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为10$\sqrt{5}$.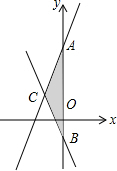 如图,已知,直线y=2x+3与直线y=-2x-1,求△ABC的面积.
如图,已知,直线y=2x+3与直线y=-2x-1,求△ABC的面积.