题目内容
19.方程(m+2)x|m|+mx-8=0是关于x的一元二次方程,则( )| A. | m=±2 | B. | m=2 | C. | m=-2 | D. | m≠±2 |
分析 根据一元二次方程的定义求解,可得答案.
解答 解:由(m+2)x|m|+mx-8=0是关于x的一元二次方程,得
$\left\{\begin{array}{l}{m+2≠0}\\{|m|=2}\end{array}\right.$.
解得m=2,
故选:B.
点评 本题利用了一元二次方程的概念.只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程,一般形式是ax2+bx+c=0(且a≠0).特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.去年我市投入使用公共自行车,受到广大市民的欢迎,截止2015年3月底已办卡27000多张,27000这个数据用科学记数法表示为( )
| A. | 0.27×105 | B. | 27×103 | C. | 2.7×103 | D. | 2.7×104 |
7.若点M(x,y)满足(x+y)2=x2+y2-2,则点M所在的象限是( )
| A. | 第一象限或第三象限 | B. | 第一象限或第二象限 | ||
| C. | 第二象限或第四象限 | D. | 不能确定 |
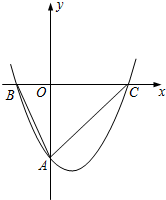 如图,已知抛物线y=ax2+bx+c经过点A(0,-4),点B(-2,0),点C(4,0).
如图,已知抛物线y=ax2+bx+c经过点A(0,-4),点B(-2,0),点C(4,0). 如图,矩形ABCD对角线AC=10,BC=6,则图中四个小矩形的周长和为28.
如图,矩形ABCD对角线AC=10,BC=6,则图中四个小矩形的周长和为28. 已知:如图,矩形ABCD的对角线AB、BD相交于点O,DE∥CA,AE∥BD.求证:四边形AODE是菱形.
已知:如图,矩形ABCD的对角线AB、BD相交于点O,DE∥CA,AE∥BD.求证:四边形AODE是菱形. 秒1个单位的速度向右平移,经过3秒该直线可将?OABC的面积平分.
秒1个单位的速度向右平移,经过3秒该直线可将?OABC的面积平分.