题目内容
8.如图,在直角坐标系中,?OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每 秒1个单位的速度向右平移,经过3秒该直线可将?OABC的面积平分.
秒1个单位的速度向右平移,经过3秒该直线可将?OABC的面积平分.
分析 若该直线可将?OABC的面积平分,则需经过此平行四边形的对称中心,设M为平行四边形ABCD的对称中心,利用O和B的坐标可求出其对称中心,进而可求出直线运动的时间.
解答 解:∵四边形ABCD是平行四边形,且点B(6,2),
∴平行四边形ABCD的对称中心M的坐标为(3,1),
∵直线的表达式为y=2x+1,
设直线平移后将?OABC平分时的直线方程为y=2x+b,
将(3,1)带入y=2x+b得b=-5,即平分时的直线方程为y=2x-5,
∴直线y=2x-5和x轴的交点坐标为($\frac{5}{2}$,0),
∵直线y=2x+1和x轴交点坐标为(-$\frac{1}{2}$,0),
∴直线运动的距离为$\frac{5}{2}$+$\frac{1}{2}$=3,
∴经过3秒的时间直线可将?OABC的面积平分.
故答案为:3.
点评 本题考查了平行四边形的性质以及直线和坐标轴的交点坐标的求法,解题的关键是掌握直线将?OABC的面积平分,则需经过此平行四边形的对称中心.

练习册系列答案
相关题目
19.方程(m+2)x|m|+mx-8=0是关于x的一元二次方程,则( )
| A. | m=±2 | B. | m=2 | C. | m=-2 | D. | m≠±2 |
16.下列说法中正确的是( )
| A. | 两条对角线垂直的四边形的菱形 | |
| B. | 对角线垂直且相等的四边形是正方形 | |
| C. | 两条对角线相等的四边形是矩形 | |
| D. | 两条对角线相等的平行四边形是矩形 |
3.下列各式:$\frac{1}{5}$(1-x),$\frac{4x}{π-3}$,$\frac{{x}^{2}-{y}^{2}}{2}$,$\frac{1+a}{b}$,$\frac{5{x}^{2}}{y}$,其中分式共有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
13.若x轴上的点P到y轴的距离为3,则点P的坐标为( )
| A. | (0,3) | B. | (0,3)或(0,-3) | C. | (3,0) | D. | (3,0)或(-3,0) |
20.下列等式由左边到右边的变形中,属于因式分解的是( )
| A. | (a+1)(a-1)=a2-1 | B. | a2-6a+9=(a-3)2 | ||
| C. | x2+2x+1=x(x+2)+1 | D. | -18x4y3=-6x2y2•3x2y |
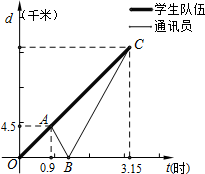 一队学生从学校出发去劳动基地军训,行进的路程与时间的图象如图所示,队伍走了0.9小时后,队伍中的通讯员按原路加快速度返回学校拿材料,通讯员经过0.5小时后回到学校,然后随即按原来加快的速度追赶队伍,恰好在劳动基地追上学生队伍.设学生队伍与学校的距离为d1,通讯员与学校的距离为d2,试根据图象解决下列问题:
一队学生从学校出发去劳动基地军训,行进的路程与时间的图象如图所示,队伍走了0.9小时后,队伍中的通讯员按原路加快速度返回学校拿材料,通讯员经过0.5小时后回到学校,然后随即按原来加快的速度追赶队伍,恰好在劳动基地追上学生队伍.设学生队伍与学校的距离为d1,通讯员与学校的距离为d2,试根据图象解决下列问题: 如图,正方形ABCD的周长为20cm,则矩形EFCG的周长是10cm.
如图,正方形ABCD的周长为20cm,则矩形EFCG的周长是10cm.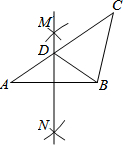 在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )