题目内容
9.已知Rt△ABC的三边AC=6cm,BC=8cm,AB=10cm,则AB边上的中线为5cm,AB边上的高为4.8cm.分析 首先根据勾股定理的逆定理得出斜边为AB,再利用直角三角形斜边上的中线等于斜边的一半得出AB边上的中线为5cm,然后利用“面积法”来求AB边上的高.
解答 解:∵Rt△ABC的三边AC=6cm,BC=8cm,AB=10cm,
∴AB2=AC2+BC2,∠C=90°,
∴AB边上的中线为$\frac{1}{2}$AB=5cm.
∵$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•AB边上的高,
∴AB边上的高=$\frac{AC•BC}{AB}$=$\frac{6×8}{10}$=4.8.
故答案为5,4.8.
点评 本题考查了勾股定理的逆定理,直角三角形斜边上的中线的性质,三角形的面积,是基础知识要熟练掌握.勾股的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
20.到x轴的距离为3的点的坐标可能是( )
| A. | (3,1) | B. | (-3,1) | C. | (1,-3) | D. | (3,2) |
14.如果点P位于x轴下方、y轴右侧,距离x轴5个单位长度,距离y轴3个单位长度,那么点P的坐标为( )
| A. | (5,-3) | B. | (3,-5) | C. | (-5,3) | D. | (-3,5) |
19.方程(m+2)x|m|+mx-8=0是关于x的一元二次方程,则( )
| A. | m=±2 | B. | m=2 | C. | m=-2 | D. | m≠±2 |
 如图,在直径为12的半圆中,点C、D为半圆的三等分点,求图中阴影部分的面积.
如图,在直径为12的半圆中,点C、D为半圆的三等分点,求图中阴影部分的面积.
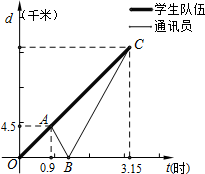 一队学生从学校出发去劳动基地军训,行进的路程与时间的图象如图所示,队伍走了0.9小时后,队伍中的通讯员按原路加快速度返回学校拿材料,通讯员经过0.5小时后回到学校,然后随即按原来加快的速度追赶队伍,恰好在劳动基地追上学生队伍.设学生队伍与学校的距离为d1,通讯员与学校的距离为d2,试根据图象解决下列问题:
一队学生从学校出发去劳动基地军训,行进的路程与时间的图象如图所示,队伍走了0.9小时后,队伍中的通讯员按原路加快速度返回学校拿材料,通讯员经过0.5小时后回到学校,然后随即按原来加快的速度追赶队伍,恰好在劳动基地追上学生队伍.设学生队伍与学校的距离为d1,通讯员与学校的距离为d2,试根据图象解决下列问题: