题目内容
13.计算:(1)$\sqrt{2\frac{1}{2}}$÷3$\sqrt{28}$×(-5$\sqrt{2\frac{2}{7}}$);
(2)$\frac{2}{y}$$\sqrt{x{y}^{5}}$•(-$\frac{3}{2}$$\sqrt{{x}^{3}y}$)÷($\frac{1}{3}$$\sqrt{\frac{y}{x}}$)
分析 先进行二次根式的化简,再结合二次根式乘除法的运算法则进行求解即可.
解答 解:(1)原式=$\frac{\sqrt{10}}{2}$÷6$\sqrt{7}$×(-5×$\frac{4}{\sqrt{7}}$)
=$\frac{\sqrt{10}}{12\sqrt{7}}$×(-5×$\frac{4}{\sqrt{7}}$)
=-$\frac{20\sqrt{10}}{84}$
=-$\frac{5\sqrt{10}}{21}$.
(2)原式=$\frac{2}{y}$×y2×$\sqrt{xy}$×(-$\frac{3}{2}$x$\sqrt{xy}$)÷$\frac{\sqrt{xy}}{3x}$
=2y$\sqrt{xy}$×(-$\frac{3}{2}$x$\sqrt{xy}$)÷$\frac{\sqrt{xy}}{3x}$
=-3x2y2÷$\frac{\sqrt{xy}}{3x}$
=-9x3y$\sqrt{xy}$.
点评 本题考查了二次根式的乘除法,解答本题的关键在于熟练掌握二次根式的化简及二次根式乘除法的运算法则.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
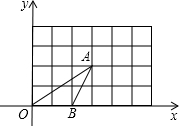 如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.
如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.
 已知有理数a、b在数轴上的位置如图,则比较a、b、-a、-b的大小为a<-b<b<-a.
已知有理数a、b在数轴上的位置如图,则比较a、b、-a、-b的大小为a<-b<b<-a. 如图一根木棒放在数轴上,数轴的1个单位长度为1cm,木棒的左端与数轴上的点A重合,右端与点B重合.
如图一根木棒放在数轴上,数轴的1个单位长度为1cm,木棒的左端与数轴上的点A重合,右端与点B重合.