题目内容
如图，则∠A+∠B+∠C+∠D+∠E=（ ）| A、240° | B、360° |
| C、540° | D、180° |
考点：三角形内角和定理
专题：
分析：延长BD与AC相交于F，根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠1、∠2，再根据三角形的内角和定理列式计算即可得解．
解答：
解：延长BD与AC相交于F，
由三角形的外角性质得，∠1=∠A+∠B，
∠2=∠BDE+∠E，
∵∠1+∠2+∠C=180°，
∴∠A+∠B+∠C+∠D+∠E=180°．
故选D．
解：延长BD与AC相交于F，由三角形的外角性质得，∠1=∠A+∠B，
∠2=∠BDE+∠E，
∵∠1+∠2+∠C=180°，
∴∠A+∠B+∠C+∠D+∠E=180°．
故选D．
点评：本题考查了三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质并作辅助线是解题的关键．
练习册系列答案
相关题目
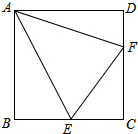如图，点E和点F分别是正方形ABCD中BC边和CD边上的点，且∠EAF=45°，则
如图，DE⊥AB于E，∠A=25°，∠D=45°，求∠ACB的度数．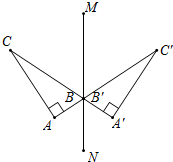
如图，Rt△ABC关于直线MN的对称点分别为A′、B′、C′，其中∠A=90°，AC=8cm，A′C=12cm．下列各代数式中是分式的是（ ）
| A、2+x | ||
B、
| ||
C、
| ||
D、
|