题目内容
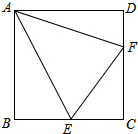 如图,点E和点F分别是正方形ABCD中BC边和CD边上的点,且∠EAF=45°,则
如图,点E和点F分别是正方形ABCD中BC边和CD边上的点,且∠EAF=45°,则| EF |
| AB |
考点:旋转的性质,全等三角形的判定与性质,勾股定理,正方形的性质
专题:计算题
分析:设正方形的边长为1,根据正方形的性质得AD=AB,∠BAD=90°,则可把△ADF绕点A顺时针旋转90°得到△ABP,如图,根据旋转的性质得AF=AP,DF=PB,∠FAP=90°,∠ABP=∠D=90°,则点P、B、C共线,再利用“SAS”证明△AEP≌△AEF,得到EF=EP,易得△CEF的周长=2,设CE=x,EF=y,CF=2-x-y,
利用勾股定理得x2+(2-x-y)2=y2,整理得x2+(y-2)x+2-2y=0,根据判别式的意义有△=(y+2)2-8≥0,解得y≥2
-2,即EF的最小值为2
-2,
所以可得
的最小值为2
-2.
利用勾股定理得x2+(2-x-y)2=y2,整理得x2+(y-2)x+2-2y=0,根据判别式的意义有△=(y+2)2-8≥0,解得y≥2
| 2 |
| 2 |
所以可得
| EF |
| AB |
| 2 |
解答:解:设正方形的边长为1,
∵四边形ABCD为正方形,
∴AD=AB,∠BAD=90°,
∴将△ADF绕点A顺时针旋转90°得到△ABP,如图,
∴AF=AP,DF=PB,∠FAP=90°,∠ABP=∠D=90°,
∴点P、B、C共线,
∵∠FAE=45°,
∴∠PAE=45°,
在△AEP和△AEF中,
,
∴△AEP≌△AEF(SAS),
∴EF=EP,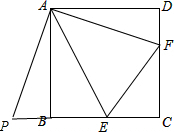
而EP=EB+BP=EB+DF,
∴EF=EB+FD,
∴△CEF的周长=EF+CE+CF=BE+EC+CF+FD=2BC=2,
设CE=x,EF=y,CF=2-x-y,
∵CE2+CF2=EF2,
∴x2+(2-x-y)2=y2,
整理得x2+(y-2)x+2-2y=0,
△=(y-2)2-4(2-2y)
=(y+2)2-8≥0,
而y>0,
∴y≥2
-2,
∴EF的最小值为2
-2,
∴
的最小值为2
-2.
故答案为2
-2.
∵四边形ABCD为正方形,
∴AD=AB,∠BAD=90°,
∴将△ADF绕点A顺时针旋转90°得到△ABP,如图,
∴AF=AP,DF=PB,∠FAP=90°,∠ABP=∠D=90°,
∴点P、B、C共线,
∵∠FAE=45°,
∴∠PAE=45°,
在△AEP和△AEF中,
|
∴△AEP≌△AEF(SAS),
∴EF=EP,

而EP=EB+BP=EB+DF,
∴EF=EB+FD,
∴△CEF的周长=EF+CE+CF=BE+EC+CF+FD=2BC=2,
设CE=x,EF=y,CF=2-x-y,
∵CE2+CF2=EF2,
∴x2+(2-x-y)2=y2,
整理得x2+(y-2)x+2-2y=0,
△=(y-2)2-4(2-2y)
=(y+2)2-8≥0,
而y>0,
∴y≥2
| 2 |
∴EF的最小值为2
| 2 |
∴
| EF |
| AB |
| 2 |
故答案为2
| 2 |
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了勾股定理、全等三角形的判定与性质和正方形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,则∠A+∠B+∠C+∠D+∠E=( )
如图,则∠A+∠B+∠C+∠D+∠E=( )| A、240° | B、360° |
| C、540° | D、180° |
为了了解福州一中初一年级学生半期考的数学成绩,从中抽样调查了100名学生半期考的数学成绩,这项调查中的样本是( )
| A、初一年级全体学生半期考的数学成绩 |
| B、从中抽取的100名学生 |
| C、从中抽取的100名学生半期考的数学成绩 |
| D、500 |
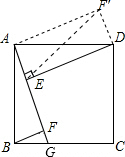 如图,四边形ABCD是正方形,F是BC上任意一点,AB=3,BF⊥AG,DE⊥AG,将△AFB旋转到△AF′D,AF′=AF,则FE=
如图,四边形ABCD是正方形,F是BC上任意一点,AB=3,BF⊥AG,DE⊥AG,将△AFB旋转到△AF′D,AF′=AF,则FE=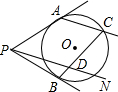 如图,PA与PB切⊙O于A、B,C为优弧
如图,PA与PB切⊙O于A、B,C为优弧
 如图,点D是△ABC的边BC上的一点,∠B=∠BAD=∠C,∠ADC=72°.
如图,点D是△ABC的边BC上的一点,∠B=∠BAD=∠C,∠ADC=72°.