题目内容
关于x的方程mx2-2(m+2)x+m+5=0无实数根,则关于x的方程(m-5)x2-2(m+2)x+m=0的根的情况是 .
考点:根的判别式
专题:计算题,分类讨论,判别式法
分析:根据关于x的方程mx2-2(m+2)x+m+5=0无实数根,可知△<0,求出m的取值范围;再根据m的值,判断出关于x的方程(m-5)x2-2(m+2)x+m=0的根的情况,要分情况讨论.
解答:解:∵关于x的方程mx2-2(m+2)x+m+5=0无实数根,
∴△=4(m+2)2-4m(m+5)<0,解得m>4,
∵当m=5时,原方程是关于x的一元一次方程,有一个实数根;
当m≠5时,原方程是关于x的一元二次方程,
∴△=4(m+2)2-4m(m-5)=16+4m,
∵m>4,
∴16+4m>0,
∴关于x的一元二次方程有两个不相等的实数根.
综上所述,关于x的方程(m-5)x2-2(m+2)x+m=0的根的情况是有一个或两个不相等的实数根.
故答案为:有一个或两个不相等的实数根.
∴△=4(m+2)2-4m(m+5)<0,解得m>4,
∵当m=5时,原方程是关于x的一元一次方程,有一个实数根;
当m≠5时,原方程是关于x的一元二次方程,
∴△=4(m+2)2-4m(m-5)=16+4m,
∵m>4,
∴16+4m>0,
∴关于x的一元二次方程有两个不相等的实数根.
综上所述,关于x的方程(m-5)x2-2(m+2)x+m=0的根的情况是有一个或两个不相等的实数根.
故答案为:有一个或两个不相等的实数根.
点评:本题考查了根的判别式,要知道,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
下列语句表示命题的是( )
| A、作∠A的平分线 |
| B、直角都相等吗? |
| C、画一条直线 |
| D、内错角不相等 |
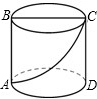 如图,一圆柱体的底面周长为24cm,高AB为4cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是
如图,一圆柱体的底面周长为24cm,高AB为4cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是 如图所示,用长10m的铝合金条制成下部为矩形,上部为半圆的窗框(包括窗棂).若使此窗户的透光面积最大,则最大透光面积为
如图所示,用长10m的铝合金条制成下部为矩形,上部为半圆的窗框(包括窗棂).若使此窗户的透光面积最大,则最大透光面积为