Question

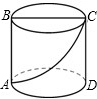如图，一圆柱体的底面周长为24cm，高AB为4cm，BC是直径，一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是

 

．

Answer 1

考点：平面展开-最短路径问题

专题：计算题

分析：将圆柱的侧面展开，得到一个长方体，再然后利用两点之间线段最短解答．

解答：解：如图所示：
由于圆柱体的底面周长为24cm，
则AD=24×

1

2

=12（cm）．
又因为CD=4cm，
所以AC=

122+42

=4

10

（cm）．
此时考虑从A-B-C线路这一情况，BC=

24

π

，AB=4，
所以这一线路的路程为

24

π

+4≈11.64＜4

10

故蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是（

24

π

+4）cm．
故答案为：（

24

π

+4）cm．

点评：此题主要考查了平面展开图的最短路径问题，将圆柱的侧面展开，构造出直角三角形是解题的关键．