题目内容
18.若a、b为一等腰三角形的边长,且满足$\sqrt{3a-6}$+$\sqrt{2-a}$=b-4,求此等腰三角形的周长.分析 由二次根式有意义的条件得$\left\{\begin{array}{l}{3a-6≥0}\\{2-a≥0}\end{array}\right.$,从而求得a的值,再代回等式求得b的值,根据等腰三角形的性质分类讨论,依据三角形三边间的关系判断能否构成三角形,从而得出其周长.
解答 解:根据题意得$\left\{\begin{array}{l}{3a-6≥0}\\{2-a≥0}\end{array}\right.$,
解得:a=2,
当a=2时,b-4=0,即b=4,
当等腰三角形三边的长度为2、2、4时,2+2=4,不能构成三角形,舍去;
当等腰三角形三边的长度为2、4、4时,2+4>4,可以构成三角形,此时周长为10.
∴此等腰三角形的周长为10.
点评 本题主要考查二次根式有意义的条件、解不等式组、等腰三角形的性质及三角形三边间的关系,根据二次根式有意义的条件得出a、b的值是解题的关键.

练习册系列答案
相关题目
7.下列各数中:+(-5)、|-1-2|、-$\frac{π}{2}$、-(-7)、0、(-2015)3,负数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
8. 如图,有理数a、b、c、d在数轴上的对应点分别是A、B、C、D,若a、c互为相反数,则b+d( )
如图,有理数a、b、c、d在数轴上的对应点分别是A、B、C、D,若a、c互为相反数,则b+d( )
 如图,有理数a、b、c、d在数轴上的对应点分别是A、B、C、D,若a、c互为相反数,则b+d( )
如图,有理数a、b、c、d在数轴上的对应点分别是A、B、C、D,若a、c互为相反数,则b+d( )| A. | 小于0 | B. | 大于0 | C. | 等于0 | D. | 不确定 |
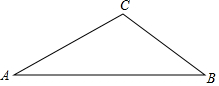 如图,在△ABC中,∠A=30°,cosB=$\frac{4}{5}$,AC=6$\sqrt{3}$.求AB的长.
如图,在△ABC中,∠A=30°,cosB=$\frac{4}{5}$,AC=6$\sqrt{3}$.求AB的长. 如图,利用标杆BE测量建筑物DC的高度,如果标杆BE长为1.5米,测得AB=2米,BC=8米,且点A、E、D在一条直线上,则楼高CD是7.5米.
如图,利用标杆BE测量建筑物DC的高度,如果标杆BE长为1.5米,测得AB=2米,BC=8米,且点A、E、D在一条直线上,则楼高CD是7.5米.