题目内容
11.填空:| 一元二次方程 | b2-4ac的值 | 方程根的情况 |
| x2-3x-6=0 | 33 | 两个不相等的实数根 |
| x2-4x=3 | 28 | 两个不相等的实数根 |
| x2+9=6x | 0 | 两个相等的实数根 |
| -2x2=3x+2 | -7 | 没有实数根 |
| x2-2$\sqrt{2}$ | 无 | 无 |
| 2x2-3=x2-2x | 16 | 两个不相等的实数根 |
分析 把a,b,c代入判别式△=b2-4ac进行计算,然后根据计算结果判断方程根的情况即可.
解答 解:填表如下:
| 一元二次方程 | b2-4ac的值 | 方程根的情况 |
| x2-3x-6=0 | 33 | 两个不相等的实数根 |
| x2-4x=3 | 28 | 两个不相等的实数根 |
| x2+9=6x | 0 | 两个相等的实数根 |
| -2x2=3x+2 | -7 | 没有实数根 |
| x2-2$\sqrt{2}$ | 无 | 无 |
| 2x2-3=x2-2x | 16 | 两个不相等的实数根 |
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (1)已知A、B、C三点如图所示,画直线AB、线段AC、射线BC,过点C画AB的垂线段CD;
(1)已知A、B、C三点如图所示,画直线AB、线段AC、射线BC,过点C画AB的垂线段CD;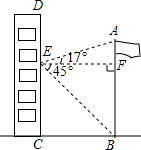 如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).
如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).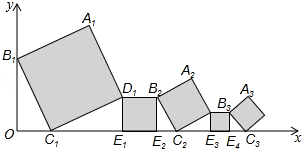 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上且坐标是(0,2),点C1、E1、E2、C2、E3、E4、C3在x轴上,C1的坐标是(1,0).B1C1∥B2C2∥B3C3,以此继续下去,则点A4到x轴的距离是$\frac{3}{8}$.
已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上且坐标是(0,2),点C1、E1、E2、C2、E3、E4、C3在x轴上,C1的坐标是(1,0).B1C1∥B2C2∥B3C3,以此继续下去,则点A4到x轴的距离是$\frac{3}{8}$. 如图Rt△ABC,∠C=Rt∠,AB=13,BC=5,若动点P在边AB上移动,则线段CP的最小值是$\frac{60}{13}$.
如图Rt△ABC,∠C=Rt∠,AB=13,BC=5,若动点P在边AB上移动,则线段CP的最小值是$\frac{60}{13}$.