题目内容
甲、乙两地的距离为10km,现在要在甲、乙两地附近建一个商场,则商场与甲、乙两地的距离之和的最小值为( )
| A、5km | B、10km |
| C、15km | D、不能确定 |
考点:三角形三边关系
专题:
分析:根据题意结合已知条件,运用三角形的三边关系问题即可解决.
解答:解:若商场建在甲、乙两地所在直线的一旁,则甲、乙两地和商场构成了一个三角形,
根据三角形的任意两边之和大于第三边,任意两边之差小于第三边的规律,
商场与甲、乙两地的距离之和大于10km;
只有当商场建在甲、乙两地之间时,商场与甲、乙两地的距离之和的最小,
最小值为10km.
故选B.
根据三角形的任意两边之和大于第三边,任意两边之差小于第三边的规律,
商场与甲、乙两地的距离之和大于10km;
只有当商场建在甲、乙两地之间时,商场与甲、乙两地的距离之和的最小,
最小值为10km.
故选B.
点评:该命题考查了三角形的三边关系在现实生活中获得实际应用问题;解题的关键是灵活运用有关知识来分析、判断或解答.

练习册系列答案
相关题目
下列关于角的说法正确的是( )
| A、角是由两条射线组成的图形 |
| B、角的边越长,角越大 |
| C、在角一边延长线上取一点 |
| D、角可以看作由一条射线绕着它的端点旋转而形成的图形 |
 如图,等腰梯形ABCD中,AD∥BC,将其中一条对角线BD平移到CE的位置,则:
如图,等腰梯形ABCD中,AD∥BC,将其中一条对角线BD平移到CE的位置,则: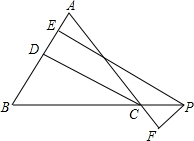 如图,在△ABC中,AB=AC,PE⊥AB,PF⊥AC,CD⊥AB,垂足分别为E、D、F,求证:PE-PF=CD.
如图,在△ABC中,AB=AC,PE⊥AB,PF⊥AC,CD⊥AB,垂足分别为E、D、F,求证:PE-PF=CD.