题目内容
 如图:在△ABC中,∠C=90°,BC=
如图:在△ABC中,∠C=90°,BC=| 3 |
考点:旋转的性质
专题:计算题
分析:先利用勾股定理计算出AB=2,然后利用中心对称的性质求解.
解答:解:在△ABC中,∵∠C=90°,BC=
,AC=1,
∴AB=
=2,
∵△ABC绕顶点A旋转180°后,点B落在点B′处,
∴AB=AB′=2,∠BAB′=180°,
∴BB′=2AB=4.
故答案为:4.
| 3 |
∴AB=
| AC2+BC2 |
∵△ABC绕顶点A旋转180°后,点B落在点B′处,
∴AB=AB′=2,∠BAB′=180°,
∴BB′=2AB=4.
故答案为:4.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=DAE=90°,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=DAE=90°,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
 如图所示,O为边长为a的正方形ABCD的中心,将一块直角边大于a的三角板的直角顶点放在O处,并将三角板绕O旋转,求证:ED+DF=a.
如图所示,O为边长为a的正方形ABCD的中心,将一块直角边大于a的三角板的直角顶点放在O处,并将三角板绕O旋转,求证:ED+DF=a.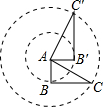 如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=2,BC=4,则弧CC′的长为
如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=2,BC=4,则弧CC′的长为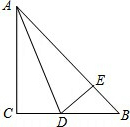 如图所示,在等腰直角△ABC中∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E.若AB=10cm,则△DEB的周长为
如图所示,在等腰直角△ABC中∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E.若AB=10cm,则△DEB的周长为