题目内容
 如图所示,O为边长为a的正方形ABCD的中心,将一块直角边大于a的三角板的直角顶点放在O处,并将三角板绕O旋转,求证:ED+DF=a.
如图所示,O为边长为a的正方形ABCD的中心,将一块直角边大于a的三角板的直角顶点放在O处,并将三角板绕O旋转,求证:ED+DF=a.考点:旋转的性质,全等三角形的判定与性质
专题:证明题
分析:连结OD,OC,如图,根据正方形的性质得OD=OC,∠ADO=∠OCF=45°,∠DOC=90°,再利用等角的余角相等得∠EOD=∠FOC,然后根据“ASA”证明△EOD≌△COF,则ED=CF,由此可得ED+DF=DC=a.
解答:证明: 连结OD,OC,如图,
连结OD,OC,如图,
∵四边形ABCD是正方形,
∴OD=OC,∠ADO=∠OCF=45°,∠DOC=90°,
∵∠EOF=90°,
∴∠EOD=∠FOC,
在△ODE和△OCF中,
,
∴△EOD≌△COF(ASA),
∴ED=CF,
而DF+CF=CD=a,
∴ED+DF=a.
 连结OD,OC,如图,
连结OD,OC,如图,∵四边形ABCD是正方形,
∴OD=OC,∠ADO=∠OCF=45°,∠DOC=90°,
∵∠EOF=90°,
∴∠EOD=∠FOC,
在△ODE和△OCF中,
|
∴△EOD≌△COF(ASA),
∴ED=CF,
而DF+CF=CD=a,
∴ED+DF=a.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各组数分别表示三条线段的长度,不能组成三角形的是( )
| A、1,2,2 |
| B、3,5,7 |
| C、三条线段的比为4:7:6 |
| D、4cm,8cm,16cm |
已知点A(2a+3b,-2)和点B(8,2a+4b)关于原点对称,那么a+b的值为( )
| A、6 | B、10 | C、-9 | D、-16 |
 已知:如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°,求证:①AC=BD;②∠APB=50°.
已知:如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°,求证:①AC=BD;②∠APB=50°. 如图:在△ABC中,∠C=90°,BC=
如图:在△ABC中,∠C=90°,BC=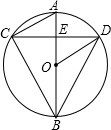 如图,已知:在⊙O中,AB是⊙O的直径,弦CD垂直平分OA,垂足为E,连接AC、BC、BD、OD.
如图,已知:在⊙O中,AB是⊙O的直径,弦CD垂直平分OA,垂足为E,连接AC、BC、BD、OD.