题目内容
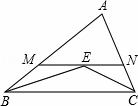
如图,中间用相同的白色正方形瓷砖,四周用相同的黑色长方形瓷砖铺设矩形地面,请观察图形并解答下列问题.
(1)问:在第6个图中,黑色瓷砖有__________块,白色瓷砖有__________块;
(2)某商铺要装修,准备使用边长为1米的正方形白色瓷砖和长为1米、宽为0.5米的长方形黑色瓷砖来铺地面.且该商铺按照此图案方式进行装修,瓷砖无须切割,恰好能完成铺设.已知白色瓷砖每块100元,黑色瓷砖每块50元,贴瓷砖的费用每平方米15元.经测算总费用为15180元.请问两种瓷砖各需要买多少块?

【考点】一元二次方程的应用.
【专题】几何图形问题.
【分析】(1)通过观察发现规律得出黑色瓷砖的块数可用含n的代数式表示为4(n+1),白瓷砖的块数可用含n的代数式表示为n(n+1),然后将n=6代入计算即可;
(2)设白色瓷砖的行数为n,根据总费用为15180元为等量关系列出方程求解即可.
【解答】解:(1)通过观察图形可知,当n=1时,黑色瓷砖有8块,白瓷砖2块;
当n=2时,黑色瓷砖有12块,白瓷砖6块;
当n=3时,黑色瓷砖有块,用白瓷砖12块;
则在第n个图形中,黑色瓷砖的块数可用含n的代数式表示为4(n+1),白瓷砖的块数可用含n的代数式表示为n(n+1),
当n=6时,黑色瓷砖的块数有4×(6+1)=28块,白色瓷砖有6×(6+1)=42块;
故答案为:28,42;
(2)设白色瓷砖的行数为n,根据题意,得:
100n(n+1)+50×4(n+1)+15(n+1)(n+2)=15180,
化简得:m2+3n﹣130=0,
解得n1=10,n2=﹣13(不合题意,舍去),
白色瓷砖块数为n(n+1)=110,
黑色瓷砖块数为4(n+1)=44.
答:白色瓷砖需买110块,黑色瓷砖需买44块.
【点评】此题主要考查了一元二次方程的应用,解答此题的关键是通过观察和分析,找出其中的规律.


 , 则
, 则 =
=  B.
B. 
 D.
D. 
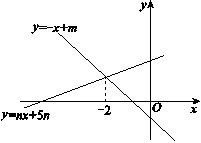
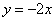 的图象沿
的图象沿 轴向上平移4个单位长度后与y轴交于点B,与x轴交于点C.
轴向上平移4个单位长度后与y轴交于点B,与x轴交于点C.
 CB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
CB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )