题目内容
16.(1)计算:|-$\sqrt{3}$|-$\sqrt{12}$+2sin60°+($\frac{1}{3}$)-1+(2-$\sqrt{3}$)0(2)先化简,再求值:$\frac{{x}^{2}-2x}{1-x}$-$\frac{1}{x-1}$,其中x=2017.
分析 (1)根据特殊角的三角函数、负整数指数幂、零指数幂和实数的加减可以解答本题;
(2)根据分式的减法可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:(1)|-$\sqrt{3}$|-$\sqrt{12}$+2sin60°+($\frac{1}{3}$)-1+(2-$\sqrt{3}$)0
=$\sqrt{3}-2\sqrt{3}+2×\frac{\sqrt{3}}{2}+3+1$
=$\sqrt{3}-2\sqrt{3}+\sqrt{3}+3+1$
=4;
(2)$\frac{{x}^{2}-2x}{1-x}$-$\frac{1}{x-1}$
=$\frac{x(x-2)}{1-x}+\frac{1}{1-x}$
=$\frac{{x}^{2}-2x+1}{1-x}$
=$\frac{(1-x)^{2}}{1-x}$
=1-x,
当x=2017时,原式=1-2017=-2016.
点评 本题考查分式的混合运算、零指数幂、负整数指数幂、特殊角的三角函数值、实数的运算,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
相关题目
6.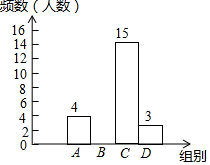 为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
(1)图中a=4,这次比赛成绩的众数落在C组;
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.
 为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题. | 组别 | 成绩x(分) | 频数(人数) |
| A | 8.0≤x<8.5 | a |
| B | 8.5≤x<9.0 | 8 |
| C | 9.0≤x<9.5 | 15 |
| D | 9.5≤x<10 | 3 |
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.
7.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 等腰直角三角形 | B. | 正三角形 | C. | 平行四边形 | D. | 矩形 |
4.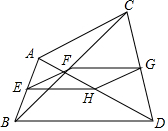 如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.
如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.
(1)求证:四边形EFGH为平行四边形.
(2)当AC=BD时,求证:四边形EFGH为菱形.
 如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.
如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.(1)求证:四边形EFGH为平行四边形.
(2)当AC=BD时,求证:四边形EFGH为菱形.
11.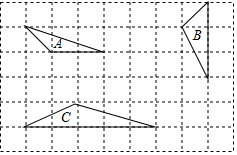 下列三个三角形中相似的是( )
下列三个三角形中相似的是( )
 下列三个三角形中相似的是( )
下列三个三角形中相似的是( )| A. | A与B | B. | A与C | C. | B与C | D. | A,B,C都相似 |
8.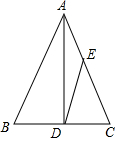 如图,已知AD是等腰△ABC底边BC上的高,sinB=$\frac{4}{5}$,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )
如图,已知AD是等腰△ABC底边BC上的高,sinB=$\frac{4}{5}$,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )
 如图,已知AD是等腰△ABC底边BC上的高,sinB=$\frac{4}{5}$,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )
如图,已知AD是等腰△ABC底边BC上的高,sinB=$\frac{4}{5}$,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{5}$ |
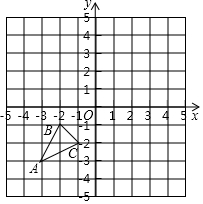 如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是平面直角坐标系上三点.
如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是平面直角坐标系上三点.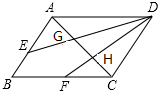 如图所示,在△ABC中,F,E分别为AB,BC的中点,G,H是AC的三等分点,EH,FG的延长线交于点D,连接AD,DC.
如图所示,在△ABC中,F,E分别为AB,BC的中点,G,H是AC的三等分点,EH,FG的延长线交于点D,连接AD,DC.