题目内容
9.已知:在△ABC中.AB、AC的垂直平分线分别交BC于点E.F.(1)如图1.∠B=∠C=30°.求∠EAF的度数.
(2)如图2.AB≠AC.且90°<∠BAC<180°
①若∠BAC=140°.则∠EAF=100°:若∠BAC=n°.则∠EAF=(n-40)°
②当∠BAC=135°时.AE⊥AF.
③若BC=a.则△AEF的周长为a.
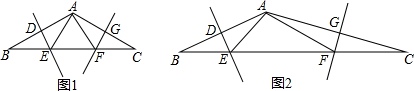
分析 (1)先根据三角形内角和定理求出∠BAC的度数,再由线段垂直平分线的性质得出AE=BE,F=CF,故可得出∠B=∠BAE,∠C=∠CAF,进而可得出结论;
(2)①根据∠BAC的度数得出∠B+∠C的度数,再由线段垂直平分线的性质得出∠BAE+∠CAF的度数,进而可得出结论;
②根据AE⊥AF可知∠EAF=90°,故可得出∠B+∠C+∠BAE+∠CAF的度数,再由线段垂直平分线的性质得出∠BAE+∠CAF的度数,进而可得出结论;
③根据线段垂直平分线的性质得出AE=BE,AF=CF,进而可得出结论.
解答 解:(1)∵∠B=∠C=30°,
∴∠BAC=180°-30°-30°=120°.
∵AB、AC的垂直平分线分别交BC于点E、F,
∴∠B=∠BAE=30°,∠C=∠CAF=30°,
∴∠EAF=120°-30°-30°=60°;
(2)①∵∠BAC=140°,
∴∠B+∠C=180°-140°=40°.
∵AB、AC的垂直平分线分别交BC于点E,F,
∴∠BAE+∠CAF=40°,
∴∠EAF=140°-40°=100°.
同理,∵∠BAC=n°,
∴∠B+∠C=180°-n°.
∵AB、AC的垂直平分线分别交BC于点E,F,
∴∠BAE+∠CAF=180°-n°,
∴∠EAF=140°-180°+n°=(n-40)°.
故答案为:100,(n-40)°;
②∵AE⊥AF,
∴∠EAF=90°,
∴∠B+∠C+∠BAE+∠CAF=180°-90°=90°.
∵AB、AC的垂直平分线分别交BC于点E,F,
∴∠B=∠BAE,∠C=∠CAF,
∴∠BAE+∠CAF=45°,
∴∠BAC=45°+90°=135°.
故答案为:135;
③∵AB、AC的垂直平分线分别交BC于点E、F,
∴AE=BE,AF=CF,
∴△AEF的周长=AE+AF+EF=BE+CF+EF=BC=a.
故答案为:a.
点评 本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

| A. | 0 | B. | 6 | C. | -6 | D. | 3 |
①两个有理数相加,和一定大于每一个加数.
②一个正数与一个负数相加得正数.
③倒数等于它本身的数仅有±1.
④两个正数相加,和为正数.
⑤两个负数相加,绝对值相减.
⑥正数加负数,其和一定等于0.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | 互为相反数 | B. | 互为倒数 | C. | 都是0 | D. | 至少有一个0 |
| A. | 3,7,15 | B. | 1,2,4 | C. | 5,5,10 | D. | 2,3,3 |
| A. | x2+3x=(x-1)2 | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | (x+1)2=x+1 |
 如图,△ABC是等边三角形,O为△ABC内任意一点,OE∥AB,OF∥AC,分别交BC于点E、F.求证:△OEF是等边三角形.
如图,△ABC是等边三角形,O为△ABC内任意一点,OE∥AB,OF∥AC,分别交BC于点E、F.求证:△OEF是等边三角形. 如图,在△ABC中,AB=10,AC=8.
如图,在△ABC中,AB=10,AC=8.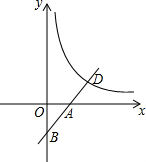 如图,一次函数y=x+b(b为常数)的图象分别交坐标轴于A,B两点,y与反比例函数y=$\frac{\sqrt{2}}{x}$(x>0)的图象交于点D,则AD•BD=2$\sqrt{2}$.
如图,一次函数y=x+b(b为常数)的图象分别交坐标轴于A,B两点,y与反比例函数y=$\frac{\sqrt{2}}{x}$(x>0)的图象交于点D,则AD•BD=2$\sqrt{2}$.