题目内容
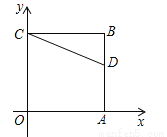
如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,10)
B.(-2,0)
C.(2,10)或(-2,0)
D.(10,2)或(-2,0)
C. 【解析】 试题解析:∵点D(5,3)在边AB上, ∴BC=5,BD=5-3=2, ①若顺时针旋转,则点D′在x轴上,OD′=2, 所以,D′(-2,0), ②若逆时针旋转,则点D′到x轴的距离为10,到y轴的距离为2, 所以,D′(2,10), 综上所述,点D′的坐标为(2,10)或(-2,0). 故选C.
练习册系列答案
相关题目


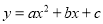 (a>0)的对称轴为直线x=1,且经过点(—1,y1),(2,y2)则试比较y1与y2的大小:y1__________y2(填“>”“<”或“=”)。
(a>0)的对称轴为直线x=1,且经过点(—1,y1),(2,y2)则试比较y1与y2的大小:y1__________y2(填“>”“<”或“=”)。
 +1)关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( )
+1)关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( ) B.
B. 
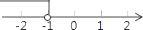 D.
D. 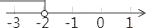
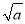 B. S的平方根是a
B. S的平方根是a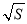
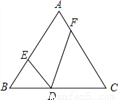
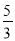
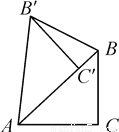
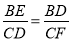 ,由已知易得:CD=BC-BD=5-1=4,由此可得:
,由已知易得:CD=BC-BD=5-1=4,由此可得: 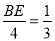 ,解得BE=
,解得BE=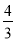 .
.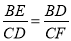 ,即
,即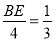 ,
,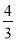 .
.