题目内容
8. 一个反比例函数的图象如图所示,则该反比例函数的解析式为( )
一个反比例函数的图象如图所示,则该反比例函数的解析式为( )| A. | y=$\frac{3}{x}$ | B. | y=-$\frac{3}{x}$ | C. | y=$\frac{3}{x}({x>0})$ | D. | y=-$\frac{3}{x}({x>0})$ |
分析 根据图示知A(1,3),将其代入反比例函数的解析式$y=\frac{k}{x}$(x>0),求得k值,进而求出反比例函数的解析式.
解答 解:设该反比例函数的解析式是$y=\frac{k}{x}$(x>0),
∵点A(1,3)在此曲线上,
∴3=k,即k=3,
∴该反比例函数的解析式为y=$\frac{3}{x}$(x>0).
故选:C.
点评 本题考查了待定系数法求反比例函数的解析式.解题时,借用了反比例函数图象上点的坐标特征,经过函数的某点一定在函数的图象上.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
19.意大利著名数学家婓波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.为了纪念这个著名的发现,人们将这组数命名为婓波那契数列.
(1)这个数列的前2014个数中,有多少个奇数?
(2)现以这组数中的各个数作为正方形的边长构造如下正方形系列:
再分别依次从左到右取2个,3个,4个,5个,…正方形拼成如下长方形并记为①、②、③、④、⑤…
(i)通过计算相应长方形的周长填写表(不计拼出的长方形内部的线段):
(ii)若按此规律继续拼成长方形,求序号为⑩的长方形周长.
(1)这个数列的前2014个数中,有多少个奇数?
(2)现以这组数中的各个数作为正方形的边长构造如下正方形系列:

再分别依次从左到右取2个,3个,4个,5个,…正方形拼成如下长方形并记为①、②、③、④、⑤…

(i)通过计算相应长方形的周长填写表(不计拼出的长方形内部的线段):
| 序号 | ① | ② | ③ | ④ | … |
| 周长 | 6 | 10 | 16 | 26 | … |
16.在同一平面直角坐标系中,若一次函数y=x-2与y=-2x+1的图象交于点M,则点M的坐标为( )
| A. | (1,1) | B. | (-1,-3) | C. | (2,0) | D. | (1,-1) |
20. 如图,已知AB是线段CD的垂直平分线,E是AB上的一点,若EC=5cm,则ED的长为( )
如图,已知AB是线段CD的垂直平分线,E是AB上的一点,若EC=5cm,则ED的长为( )
 如图,已知AB是线段CD的垂直平分线,E是AB上的一点,若EC=5cm,则ED的长为( )
如图,已知AB是线段CD的垂直平分线,E是AB上的一点,若EC=5cm,则ED的长为( )| A. | 4cm | B. | 5cm | C. | 2cm | D. | $\frac{5}{2}$cm |
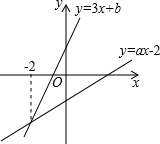 如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x=-2.
如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x=-2. 如图,AB∥CD,直线PQ交AB、CD于点M、N,ME平分∠PMB,NF平分∠PND.求证:ME∥NF.
如图,AB∥CD,直线PQ交AB、CD于点M、N,ME平分∠PMB,NF平分∠PND.求证:ME∥NF.