题目内容
5.研究下列算式,你会发现什么规律?$\sqrt{11-2}$=3,
$\sqrt{1111-22}$=33,
$\sqrt{111111-222}$=333,
…
(1)请将你找出的规律用式子表示出来;
(2)你会证明你得到的结论吗?试试看.
分析 (1)观察上述算式可发现:根号内被开方数是2n个数字1和n个数字2的差,结果为n个数字3;
(2)从已知三个等式中找出计算规律,然后应用到一般式中.
解答 解:(1)∵$\sqrt{11-2}$=3,$\sqrt{1111-22}$=33,$\sqrt{111111-222}$=333
∴可发现:根号内被开方数是2n个数字1和n个数字2的差,结果为n个数字3,
则第n个算式可表示为:$\sqrt{\underset{\underbrace{11…11}}{2n个}-\underset{\underbrace{22…2}}{n个}}=\underset{\underbrace{33…3}}{n个}$.
(2)∵$\sqrt{11-2}=\sqrt{9}=3$;
$\sqrt{1111-22}$=$\sqrt{11×(101-2)}$=$\sqrt{11×99}$=$\sqrt{11×11×9}$=11×3=33;
$\sqrt{111111-222}$=$\sqrt{111×(1001-2)}$=$\sqrt{111×999}$=$\sqrt{111×111×9}$=111×3=333;
∴$\sqrt{\underset{\underbrace{11…1}}{2n个}-\underset{\underbrace{22…2}}{n个}}$=$\sqrt{\underset{\underbrace{11…1}}{n个}×(100…1-2)}$
=$\sqrt{\underset{\underbrace{11…1}}{n个}×\underset{\underbrace{99…9}}{n个}}$
=$\sqrt{\underset{\underbrace{11…1}}{n个}×\underset{\underbrace{11…1}}{n个}×9}$
=$\underset{\underbrace{11…1}}{n个}×3$
=$\underset{\underbrace{33…3}}{n个}$.
点评 本题主要考查数字的变化规律,从已知三个等式中提取公因数再开方是证明关键.

 如图,AB为⊙O的直径,弦CD⊥AB于H,弦CE⊥BD于G,交AB于点F,下列结论不正确的是( )
如图,AB为⊙O的直径,弦CD⊥AB于H,弦CE⊥BD于G,交AB于点F,下列结论不正确的是( )| A. | CH=DH | B. | AH=FH | C. | CD=CE | D. | CF=DE |
| A. |  | B. |  | C. |  | D. |  |
 如图,已知△ABC.
如图,已知△ABC. 如图,△ABC的中线BE,CF相交于点G,P,Q分别是BG,CG的中点.
如图,△ABC的中线BE,CF相交于点G,P,Q分别是BG,CG的中点.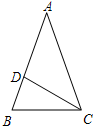 如图,在△ABC中,AB=AC,D为AB上一点,AD=CD,若∠ACD=40°,则∠B=70°.
如图,在△ABC中,AB=AC,D为AB上一点,AD=CD,若∠ACD=40°,则∠B=70°.