Question

13．如图，已知△ABC．
（1）利用直尺和圆规，按照下列要求作图（保留作图痕迹，不要求写作法）
①作∠ABC的平分线BD交AC于点D；
②作线段BD的垂直平分线分别交AB、BC于点E、F．
（2）连接DE，请判断线段DE与线段BF的数量关系，并说明理由．

Answer 1

分析 （1）直接利用角平分线的作法以及结合线段垂直平分线的画法得出答案；
（2）利用线段垂直平分线的性质结合全等三角形的判定与性质得出答案．

解答 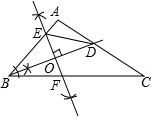解：（1）如图所示：

（2）DE=BF，
理由：∵BD平分∠ABC，
∴∠ABD=∠DBC，
∵EF垂直平分BD，设垂足为O，
则OB=OD，BE=DE，
∴∠ABD=∠EDB，
∴∠DBC=∠EDB，
在△BOF和△DOE中，
$\left\{\begin{array}{l}{∠FBO=∠EDO}\\{BO=DO}\\{∠BOF=∠DOE}\end{array}\right.$，
∴△BOF≌△DOE（ASA），
∴DE=BF．

点评 此题主要考查了线段垂直平分线的性质与画法以及全等三角形的判定与性质，正确掌握线段垂直平分线的性质是解题关键．