题目内容
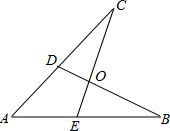 如图,已知AB=AC,要使△ABD≌△ACE,只需补充条件( )
如图,已知AB=AC,要使△ABD≌△ACE,只需补充条件( )| A、∠BOE=∠COD |
| B、∠DOE=∠BOC |
| C、BO=CO |
| D、BO⊥CO |
考点:全等三角形的判定
专题:
分析:利用对顶角相等可对A、B选项进行判断;连结BC,如图,若BO=CO,则∠1=∠2,再由AB=AC得∠ACB=∠ABC,则∠ABD=∠ACE,然后可根据“ASA”判断△ABD≌△ACE,于是可对C选项进行判断;由于BO⊥CO不能得到∠ABD=∠ACE,则可对D进行判断.
解答:解: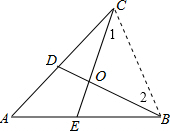 ∠BOE=∠COD,∠DOE=∠BOC,它们不需补充,所以A、B选项错误;
∠BOE=∠COD,∠DOE=∠BOC,它们不需补充,所以A、B选项错误;
连结BC,如图,
∵BO=CO,
∴∠1=∠2,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠ABD=∠ACE,
而∠BAD=∠CAE,
∴△ABD≌△ACE(ASA),所以C选项正确;
BO⊥CO不能得到∠ABD=∠ACE,所以D选项错误.
故选C.
 ∠BOE=∠COD,∠DOE=∠BOC,它们不需补充,所以A、B选项错误;
∠BOE=∠COD,∠DOE=∠BOC,它们不需补充,所以A、B选项错误;连结BC,如图,
∵BO=CO,
∴∠1=∠2,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠ABD=∠ACE,
而∠BAD=∠CAE,
∴△ABD≌△ACE(ASA),所以C选项正确;
BO⊥CO不能得到∠ABD=∠ACE,所以D选项错误.
故选C.
点评:本题考查了全等三角形的判定:可利用”SSS”、“SAS”、“ASA”、“AAS”判断两三角形全等.

练习册系列答案
相关题目
适合关系式|x+
|+|x-
|=2的整数解x的个数是( )
| 2 |
| 3 |
| 4 |
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
在-(-8),|-1|,-|-2|,(-2)3这四个数中非负数共有( )个.
| A、4 | B、3 | C、2 | D、1 |
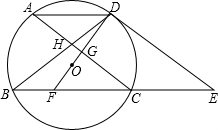 如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.
如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F. 如图,由1,2,3,…组成一个数阵,观察规律.
如图,由1,2,3,…组成一个数阵,观察规律. 将如图所示的长方体用过ABCD的平面切割,得到两个什么几何体?说出它们的名称.
将如图所示的长方体用过ABCD的平面切割,得到两个什么几何体?说出它们的名称.