题目内容
如图，AB∥CD，AD、BC交于O点，∠BAD=35°，∠BOD=75°，则∠C的度数是（ ）| A、30° | B、40° |
| C、50° | D、45° |
考点：平行线的性质,三角形内角和定理
专题：计算题
分析：根据平行线的性质得∠D=∠A=35°，然后根据三角形的外角性质得到求解．
解答：解：∵AB∥CD
∴∠D=∠A=35°，
∵∠BOD=∠C+∠D，∠BOD=75°
∴∠C=75°-35°=40°．
故选B．
∴∠D=∠A=35°，
∵∠BOD=∠C+∠D，∠BOD=75°
∴∠C=75°-35°=40°．
故选B．
点评：本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图，△ABC中，D为边AC的中点，设BD=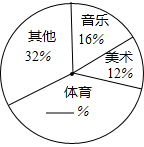
为了解某区初三学生的课余生活情况，调查小组在全区范围内随机抽取部分学生进行问卷调查．问卷中请学生选择最喜欢的课余生活种类（每人只选一类），选项有音乐类、美术类、体育类及其他共四类，调查后将数据绘制成扇形统计图（如图）．如果该区有6000名初三学生，请你估计该区最喜欢体育运动的初三学生约有下面化简正确的是（ ）
| A、2x-5xy=-3y | ||||
B、
| ||||
| C、（2x+1）2=4x2+1 | ||||
D、若x＞0，
|
下列命题正确的是（ ）
| A、垂直于半径的直线一定是圆的切线 |
| B、正三角形绕其中心旋转180°后能与原图形重合是必然事件 |
| C、有一组对边平行，一组对角相等的四边形是平行四边形 |
| D、四个角都是直角的四边形是正方形 |
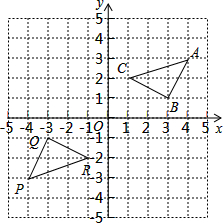如图，三角形PQR是三角形ABC经过某种变换后得到的图形，分别写出点A与点P，点B与点Q，点C与点R的坐标，并观察它们之间的关系，如果三角形ABC中任意一点M的坐标为（a，b），那么它的对应点N的坐标是什么？
张华同学家要建一个长方形的养鸡场，鸡场的一边靠墙（墙长为25米），另三边用长40米的竹篱笆围成．问长方形的鸡场的面积能否达到128m2？如果能，AB的长是多少米？如果不能，请说明理由．