题目内容
已知点E(6,m),A(4,0),B(0,2),O(0,0),且△ABE的面积是△OAB面积的3倍,求点E的坐标.
考点:坐标与图形性质,三角形的面积
专题:
分析:根据点A、B的坐标求出OA、OB,再求出△OAB的面积,然后分点E在第一象限和第四象限两种情况表示出△ABE的面积,解方程求出m的值即可.
解答: 解:∵A(4,0),B(0,2),
解:∵A(4,0),B(0,2),
∴OA=4,OB=2,
∴△OAB面积=
OA•OB=
×4×2=4,
①点E在第一象限时,△ABE的面积=
×(2+m)×6-
×2•m-4=12,
解得m=5,
②点E在第四象限时,△ABE的面积=
×(4+6)(-m)+4-
×6(2-m)=12,
解得m=-7,
所以,点E的坐标为(6,5)或(6,-7).
 解:∵A(4,0),B(0,2),
解:∵A(4,0),B(0,2),∴OA=4,OB=2,
∴△OAB面积=
| 1 |
| 2 |
| 1 |
| 2 |
①点E在第一象限时,△ABE的面积=
| 1 |
| 2 |
| 1 |
| 2 |
解得m=5,
②点E在第四象限时,△ABE的面积=
| 1 |
| 2 |
| 1 |
| 2 |
解得m=-7,
所以,点E的坐标为(6,5)或(6,-7).
点评:本题考查了坐标与图形性质,三角形的面积,难点在于分情况进行△ABE的面积的表示,作出图形更形象直观.

练习册系列答案
相关题目
 如图,AB∥CD,AD、BC交于O点,∠BAD=35°,∠BOD=75°,则∠C的度数是( )
如图,AB∥CD,AD、BC交于O点,∠BAD=35°,∠BOD=75°,则∠C的度数是( )| A、30° | B、40° |
| C、50° | D、45° |
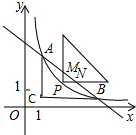 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,DE是△ABC的AB边的垂直平分线,AE平分∠BAC,∠B=30°,求∠C的度数.
如图,DE是△ABC的AB边的垂直平分线,AE平分∠BAC,∠B=30°,求∠C的度数.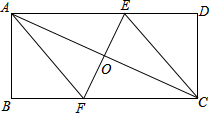 如图,在矩形ABCD中,对角线AC的垂直平分线分别交BC、AD于点F、E,垂足为O.
如图,在矩形ABCD中,对角线AC的垂直平分线分别交BC、AD于点F、E,垂足为O. 如图,在△ABC中,AB=AC,以AB边为直径作⊙O,交BC边于点D,过点D作,DF⊥AC于点F
如图,在△ABC中,AB=AC,以AB边为直径作⊙O,交BC边于点D,过点D作,DF⊥AC于点F