题目内容
20．
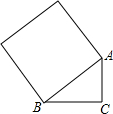如图，∠ACB=90°，AC=6，BC=8，则以AB为边长的正方形面积为100．
分析 根据已知条件，利用勾股定理求出AB的长，然后即可求出此正方形的面积．
解答 解：∵∠ACB=90°，AC=6，BC=8，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10，
∴正方形的面积是10×10=100，
故答案为：100．
点评 此题主要考查了勾股定理，关键是掌握在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
10．我市对城区某主干道进行绿化，计划在此公路的一侧全部栽上“市树”--樟树，要求路的两端各栽一棵，并且每两棵树的间隔相等．如果每隔5米栽1棵，则树苗缺21棵；如果每隔6米栽1棵，则树苗正好用完．设原有树苗x棵，则根据题意列出方程正确的是（ ）
| A． | 5（x+2）=6（x-1） | B． | 5（x+21-1）=6（x-1） | C． | 5（x+21-1）=6x | D． | 5（x+21）=6x |
．
15．下列关于二次函数y=-（x-3）2+$\frac{1}{2}$的说法，错误的是（ ）
| A． | 其对称轴为x=3 | B． | 其图象的顶点坐标为（3，$\frac{1}{2}$） | ||
| C． | 其图象开口方向向下 | D． | 其图象与y轴的交点坐标为（0，$\frac{1}{2}$） |
5．已知甲、乙、丙、丁共有30本，又知甲、乙、丙、丁的课外书制作的条形统计图的高度之比为2：3：4：1，则乙的课外书的本数为（ ）
| A． | 6本 | B． | 9本 | C． | 11本 | D． | 12本 |
9．
如图，AB∥EF∥CD，∠ABC=46°，∠CEF=160°，则∠BCE等于（ ）
如图，AB∥EF∥CD，∠ABC=46°，∠CEF=160°，则∠BCE等于（ ）| A． | 26° | B． | 16° | C． | 23° | D． | 20° |