Question

3．如图，在平面直角坐标系xOy中，直线y=kx+b与x轴相交于点C，与反比例函数在第一象限内的图象相交于点A（1，8）、B（m，2）．
（1）求该反比例函数和直线y=kx+b的表达式；
（2）求证：△OBC为直角三角形；
（3）设∠ACO=α，点Q为反比例函数在第一象限内的图象上一动点且满足90°-α＜∠QOC＜α，求点Q的横坐标q的取值范围．

Answer 1

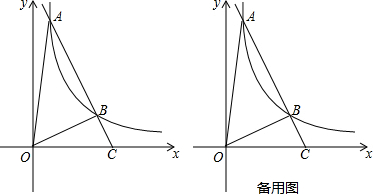
分析 （1）首先利用待定系数法求得反比例函数的解析式，然后求得B的坐标，则利用待定系数法即可求得直线的解析式；
（2）过点B作BD⊥OC于点D，在直角△OBD和直角△OBC中，利用勾股定理求得OB²和BC²，然后利用勾股定理的逆定理即可证明；
（3）分成Q在B的左侧和右侧两种情况讨论，当在右侧时一定不成立，当在左侧时，判断是否存在点Q时∠QCO=90°-α即可．

解答 解：（1）设反比例函数的解析式是y=$\frac{k}{x}$，
把（1，8）代入得k=8，
则反比例函数表达式为y=$\frac{8}{x}$，
把（m，2）代入得m=$\frac{8}{2}$=4，
则B的坐标是（4，2）．
根据题意得：$\left\{\begin{array}{l}{k+b=8}\\{4k+b=2}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-2}\\{b=10}\end{array}\right.$，
，则直线表达式y=-2x+10；
（2）过点B作BD⊥OC于点D，（图1）则D的坐标是（4，0）．
在y=-2x+10中，令y=0，解得x=5，则OC=5．
∵在直角△OBD中，BD=2，OD=OC-OD=5-5=1，
则OB²=OD²+BD²=4²+2²=20，
同理，直角△BCD中，BC²=BD²+CD²=2²+1²=5=25，
∴OB²+BC²=OC²，
∴△OBC是直角三角形；
（3）当Q在B的右侧时一定不成立．
在y=-2x+10中，令x=0，则y=10，
则当Q在的左边时，（图2）tan∠ACO=tanα=2，
则tan（90°-α）=$\frac{1}{2}$．
当∠QCO=90°-α是，Q的横坐标是p，则纵坐标是$\frac{8}{p}$，
tan∠QCO=tan（90°-α）=$\frac{8}{p}$：（5-p）=$\frac{1}{2}$．
即p²-5p+16=0，
△=25-4×16=-39＜0，则Q不存在．
故当Q在AB之间时，满足条件，
因而2＜q＜4．

点评 本题考查了待定系数法求反比例函数与一次函数的解析式以及正切函数的性质，判断Q在AB之间是关键．