题目内容
10.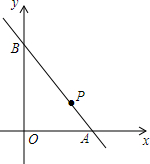 如图,直线y=-$\frac{3}{4}$x+3与x轴,y轴分别交于A、B两点,点P是线段AB的动点,若使得△OAP为等腰三角形,求点P的坐标.
如图,直线y=-$\frac{3}{4}$x+3与x轴,y轴分别交于A、B两点,点P是线段AB的动点,若使得△OAP为等腰三角形,求点P的坐标.
分析 根据题意,则OP=PA,然后根据等腰三角形的性质,求出P点的坐标即可.
解答 解:由直线y=-$\frac{3}{4}$x+3可知A(4,0),
如图2,∵△OAP为等腰三角形,
∴OP=PA,
作PE⊥x轴于点E,则OE=AE=2,
把x=2代入y=-$\frac{3}{4}$x+3得,y=$\frac{3}{2}$,
∴P点的坐标是(2,$\frac{3}{2}$).
∴若使得△OAP为等腰三角形,P(2,$\frac{3}{2}$).
点评 考查了等腰三角形的判定和性质以及一次函数图象上点的坐标特征,考查了数形结合思想的应用.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 已知:PA、PB、CD分别切⊙O于A、B、E三点,PA=6.求:
已知:PA、PB、CD分别切⊙O于A、B、E三点,PA=6.求: 已知等边三角形ABC的边长为2,将这个三角形放置在如图所示的直角坐标系中,且B,C两点的坐标分别为(-1,0),(1,0)
已知等边三角形ABC的边长为2,将这个三角形放置在如图所示的直角坐标系中,且B,C两点的坐标分别为(-1,0),(1,0)