题目内容
5.A、B、C、D、E、F是数轴上从左到右的六个点,并且AB=BC=CD=DE=EF,点A表示的数是-7,点F所表示的数是9,那么与点C所表示的数最接近的整数是多少?分析 先根据数轴上两点之间距离的定义求出AF之间的距离,再根据AB=BC=CD=DE=EF求出EF之间的距离,根据EF之间的距离即可求出C点所表示的数,进而得到答案.
解答 解:由A、F两点所表示的数可知,AF=9-(-7)=16,
∵AB=BC=CD=DE=EF,
∴EF=16÷5=3.2,
∴点C表示的数为:-7+3.2×2=-0.6;
∴与点C所表示的数最接近的整数是-1.
点评 本题考查的是数轴上两点之间距离的定义,根据A、F两点所表示的数求出AF之间的距离是解答此题的关键.

练习册系列答案
相关题目
13.在二元一次方程x+3y=1的解中,当x=4时,对应的y的值是( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -1 | D. | 4 |
20.2100×(-$\frac{1}{2}$)99=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
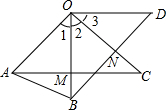 已知,OA=OB,OC=OD,∠1=∠2=∠3,AC交OB于M,BD交OC于N,求证:OM=ON.
已知,OA=OB,OC=OD,∠1=∠2=∠3,AC交OB于M,BD交OC于N,求证:OM=ON.
 如图,已知圆锥的母线长为6,侧面展开图(扇形)的面积是12π,则这个圆锥侧面展开图中弧AC的长度是4π.
如图,已知圆锥的母线长为6,侧面展开图(扇形)的面积是12π,则这个圆锥侧面展开图中弧AC的长度是4π.