题目内容
3. 如图,在△ABC中,∠ABC、∠ACB的平分线BE、CD相交于点F,∠A=60°,则∠BFC=120°.
如图,在△ABC中,∠ABC、∠ACB的平分线BE、CD相交于点F,∠A=60°,则∠BFC=120°.
分析 根据角平分线的定义可得出∠CBF=$\frac{1}{2}$∠ABC、∠BCF=$\frac{1}{2}$∠ACB,再根据内角和定理结合∠A=60°即可求出∠BFC的度数.
解答 解:∵∠ABC、∠ACB的平分线BE、CD相交于点F,
∴∠CBF=$\frac{1}{2}$∠ABC,∠BCF=$\frac{1}{2}$∠ACB,
∵∠A=60°,
∴∠ABC+∠ACB=180°-∠A=120°,
∴∠BFC=180°-(∠CBF+BCF)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=120°.
故答案为:120°.
点评 本题考查了三角形内角和定理,根据角平分线的定义结合三角形内角和定理求出角的度数是解题的关键.

练习册系列答案
相关题目
13.数轴上表示到原点的距离是6的数是( )
| A. | 3 | B. | ±3 | C. | -6 | D. | ±6 |
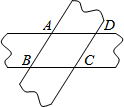 如图,将两条宽度都为6的纸片重叠在一起,使∠ABC=60°,则四边形ABCD的面积为24$\sqrt{3}$.
如图,将两条宽度都为6的纸片重叠在一起,使∠ABC=60°,则四边形ABCD的面积为24$\sqrt{3}$.