题目内容
3. 如图所示,四边形ABCD中,AD∥BC,E、F分别是两底的中点,求证:EF<$\frac{1}{2}$(AB+CD).
如图所示,四边形ABCD中,AD∥BC,E、F分别是两底的中点,求证:EF<$\frac{1}{2}$(AB+CD).
分析 取BD的中点H,连接HE、HF,根据三角形中位线定理得到EH=$\frac{1}{2}$AB,同理得到HF=$\frac{1}{2}$CD,根据三角形三边关系得到EF<EF+FH,等量代换即可.
解答 证明: 取BD的中点H,连接HE、HF,
取BD的中点H,连接HE、HF,
∵E是AD的中点,H是BD的中点,
∴EH=$\frac{1}{2}$AB,
同理,HF=$\frac{1}{2}$CD,
∵EF<EF+FH,
∴EF<$\frac{1}{2}$(AB+CD).
点评 本题考查的是三角形中位线定理和三角形三边的关系,掌握三角形的中位线平行于第三边,并且等于第三边的一半、三角形两边之和大于第三边是解题的关键.

练习册系列答案
相关题目
 如图,AB、CD相交于点E,EA=EC,AC∥BD.求证:EB=ED.
如图,AB、CD相交于点E,EA=EC,AC∥BD.求证:EB=ED.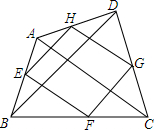 如图,在四边形ABCD中,AC=4cm,BD=5cm,E,F,G,H分别是边AB,BC,CD,DA的中点,求四边形EFGH的周长.
如图,在四边形ABCD中,AC=4cm,BD=5cm,E,F,G,H分别是边AB,BC,CD,DA的中点,求四边形EFGH的周长.