题目内容
18.已知ax=$\sqrt{2}$+1,求$\frac{{a}^{2x}-{a}^{-2x}}{{a}^{x}+{a}^{-x}}$的值.分析 由ax=$\sqrt{2}$+1,得出a-x=$\sqrt{2}$-1,由此进一步化简分式代入求得答案即可.
解答 解:∵ax=$\sqrt{2}$+1,
∴a-x=$\sqrt{2}$-1,
∴$\frac{{a}^{2x}-{a}^{-2x}}{{a}^{x}+{a}^{-x}}$
=$\frac{({a}^{x}+{a}^{-x})({a}^{x}-{a}^{-x})}{{a}^{x}+{a}^{-x}}$
=ax-a-x
=$\sqrt{2}$+1-$\sqrt{2}$+1
=2.
点评 本题主要考查分式的化简求值,掌握分式混合运算的计算方法是解决问题的关键.

练习册系列答案
相关题目
9.如果关于x的方程(m+1)x2+(m-1)x+m=0是一元一次方程,则m的值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | 1或-1 |
6.下列方程中是一元一次方程的是( )
| A. | $\frac{2}{x}$+2=5 | B. | $\frac{3x-1}{2}$+4=3x | C. | y2+3y=0 | D. | 9x-y=2 |
13.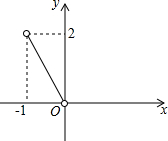 已知函数图象如图所示,则此函数解析式为( )
已知函数图象如图所示,则此函数解析式为( )
 已知函数图象如图所示,则此函数解析式为( )
已知函数图象如图所示,则此函数解析式为( )| A. | y=-2x | B. | y=-2x(-1<x<0) | C. | y=-$\frac{1}{2}$x | D. | y=-$\frac{1}{2}$x(-1<x<0) |
 如图所示,四边形ABCD中,AD∥BC,E、F分别是两底的中点,求证:EF<$\frac{1}{2}$(AB+CD).
如图所示,四边形ABCD中,AD∥BC,E、F分别是两底的中点,求证:EF<$\frac{1}{2}$(AB+CD).