Question

4．设P是高为h的正三角形内的一点，P到三边的距离分别为x，y，z（x≤y≤z）．若以x，y，z为边可以组成三角形，则z应满足的条件为（　　）

• A． $\frac{1}{4}$h≤z$＜\frac{1}{3}$h
• B． $\frac{1}{3}$h≤z$＜\frac{1}{2}$h
• C． $\frac{1}{2}$h≤z$＜\frac{3}{4}$h
• D． $\frac{3}{4}h≤z＜h$

Answer 1

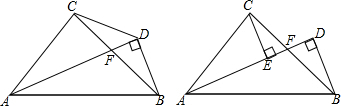
分析 如图，连接AP，BP，CP，先利用S_△ABC=S_△APC+S_△BPC+S_△APB，找出x，y，z与h的关系，再运用三角形三边关系可得z＜$\frac{1}{2}$h，由x≤y≤z可得z≥$\frac{1}{3}$h，即可求出z应满足的条件．

解答 解：如图，PE=x，PF=y，Pq=Q=z，连接AP，BP，CP，

∵S_△ABC=S_△APC+S_△BPC+S_△APB，
∴$\frac{1}{2}$BC•h=$\frac{1}{2}$AC•x+$\frac{1}{2}$BC•y+$\frac{1}{2}$AB•z，
∵△ABC为等边三角形，
∴AB=BC=AC，
∴$\frac{1}{2}$BC•h=$\frac{1}{2}$BC（x+y+z），即x+y+z=h，
∵以x，y，z为边可以组成三角形，
∴x+y＞z，
∴2z＜h，即z＜$\frac{1}{2}$h，
又∵x≤y≤z，
∴z≥$\frac{1}{3}$（x+y+z），即z≥$\frac{1}{3}$h，
∴$\frac{1}{3}$h≤z$＜\frac{1}{2}$h．
故选：B．

点评 本题主要考查了三角形边角关系，解题的关键是利用S_△ABC=S_△APC+S_△BPC+S_△APB，找出x，y，z与h的关系．