题目内容
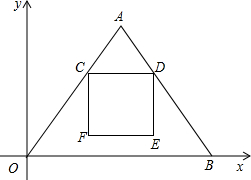如图，在平面直角坐标系xOy中，等腰△OAB的顶点A在第一象限，底边OB在x轴的正半轴上，且AO=AB=10cm，OB=12cm．动点C从点A出发，沿AO边向O点运动（不与O点重合），速度为1cm/s，运动时间为ts．过点C作CD∥OB交AB于点D．以CD为边，在点A的异侧作正方形CDEF．（1）若正方形CDEF与△OAB重叠部分的面积为S，求S关于t的函数关系式，并写出自变量t的取值范围；
（2）连接OF，当t为何值时，△OCF为等腰三角形？
考点：相似形综合题,解一元二次方程-公式法,等腰三角形的性质,勾股定理,平行四边形的判定与性质,正方形的性质,相似三角形的判定与性质
专题：综合题,分类讨论
分析：（1）首先考虑点F在OB上时所对应的S和t的值，然后分别对点F在△OAB内部、外部进行讨论，就可解决问题．
（2）由于△OCF为等腰三角形时腰并不确定，因此可分三种情况（①FO=FC，②CO=CF，③OC=OF）进行讨论，只需根据线段之间的数量关系建立关于t的方程，就可解决问题．
（2）由于△OCF为等腰三角形时腰并不确定，因此可分三种情况（①FO=FC，②CO=CF，③OC=OF）进行讨论，只需根据线段之间的数量关系建立关于t的方程，就可解决问题．
解答：解：（1）①当点F在OB上时，
过点A作AH⊥OB于H，交CD于G，如图1①．
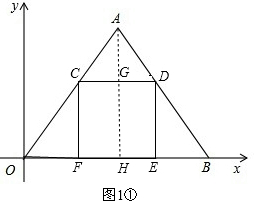
则有∠AHE=90°．
∵四边形CDEF是正方形，
∴CD=CF，∠DCF=∠CFE=90°．
∴∠AHE=∠CFE=90°．
∴CF∥GH．
∴∠AGC=∠DCF=90°．
∴AG⊥CD．
∵CD∥OB，CF∥GH，
∴四边形CGHF是平行四边形．
∴CF=GH．
∵AO=AB，AH⊥OB，
∴OH=BH=
OB=6．
∵∠AHO=90°，OA=10，OH=6，
∴AH=8．
设正方形CDEF的边长为x，
则GH=CF=CD=x，AG=AH-GH=8-x．
∵CD∥OB，∴△ACD∽△AOB．
∵AG⊥CD，AH⊥OB，
∴
=
=
．
∴
=
=
．
解得：x=
，t=4．
∴S=
．
②当点F在△OAB内部时，0＜t＜4，如图1②．
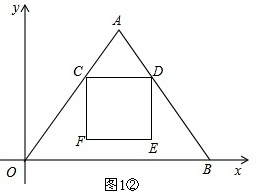
∵△ACD∽△AOB，
∴
=
．
∴
=
．
∴CD=
．
∴S=CD2=
．
③当点F在△OAB外部时，4＜t＜10，
过点A作AH⊥OB于H，如图1③．
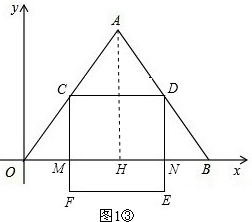
则有CD=
，OC=10-t，AH=8，CM∥AH．
∴△OMC∽△OHA．
∴
=
=
．
∴
=
=
．
∴CM=8-
，OM=6-
．
∴S=CD•CM=
•（8-
）=-
t2+
t．
综上所述：当0＜t≤4时，S=
；当4＜t＜10时，S=-
t2+
t．
（2）①若FO=FC，如图2①．
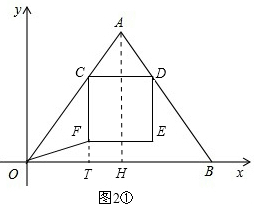
此时点F在△OAB内部，0＜t＜4．
过点A作AH⊥OB于H，延长CF交OB于点T，
由（1）得：CF=CD=
，CT=8-
，OT=6-
．
则FT=CT-CF=8-
-
=8-2t．
∵∠FTO=90°，∴FT2+OT2=OF2．
∴（8-2t）2+（6-
）2=（
）2．
整理得：73t2-980t+2500=0．
解得：t1=
，t2=10．
∵0＜t＜4，∴t=
．
②若CO=CF，如图2②．
此时点F在△OAB外部，4＜t＜10．
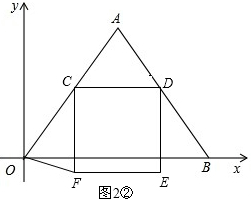
∵CF=CD=
，OC=10-t，CF=CO，
∴
=10-t．
解得：t=
．
③若OC=OF，如图2③．
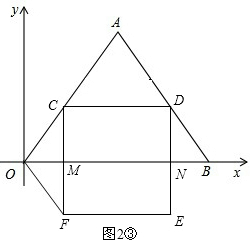
此时点F在△OAB外部，4＜t＜10．
则有CM=8-
，CF=CD=
．
∵OC=OF，OM⊥CF，
∴CM=FM=
CF．
∴8-
=
×
．
解得：t=
．
综上所述：当t为
秒或
秒或
秒时，△OCF为等腰三角形．
过点A作AH⊥OB于H，交CD于G，如图1①．
则有∠AHE=90°．
∵四边形CDEF是正方形，
∴CD=CF，∠DCF=∠CFE=90°．
∴∠AHE=∠CFE=90°．
∴CF∥GH．
∴∠AGC=∠DCF=90°．
∴AG⊥CD．
∵CD∥OB，CF∥GH，
∴四边形CGHF是平行四边形．
∴CF=GH．
∵AO=AB，AH⊥OB，
∴OH=BH=
| 1 |
| 2 |
∵∠AHO=90°，OA=10，OH=6，
∴AH=8．
设正方形CDEF的边长为x，
则GH=CF=CD=x，AG=AH-GH=8-x．
∵CD∥OB，∴△ACD∽△AOB．
∵AG⊥CD，AH⊥OB，
∴
| AG |
| AH |
| CD |
| OB |
| AC |
| AO |
∴
| 8-x |
| 8 |
| x |
| 12 |
| t |
| 10 |
解得：x=
| 24 |
| 5 |
∴S=
| 576 |
| 25 |
②当点F在△OAB内部时，0＜t＜4，如图1②．
∵△ACD∽△AOB，
∴
| CD |
| OB |
| AC |
| AO |
∴
| CD |
| 12 |
| t |
| 10 |
∴CD=
| 6t |
| 5 |
∴S=CD2=
| 36t2 |
| 25 |
③当点F在△OAB外部时，4＜t＜10，
过点A作AH⊥OB于H，如图1③．
则有CD=
| 6t |
| 5 |
∴△OMC∽△OHA．
∴
| CM |
| AH |
| OM |
| OH |
| OC |
| OA |
∴
| CM |
| 8 |
| OM |
| 6 |
| 10-t |
| 10 |
∴CM=8-
| 4t |
| 5 |
| 3t |
| 5 |
∴S=CD•CM=
| 6t |
| 5 |
| 4t |
| 5 |
| 24 |
| 25 |
| 48 |
| 5 |
综上所述：当0＜t≤4时，S=
| 36t2 |
| 25 |
| 24 |
| 25 |
| 48 |
| 5 |
（2）①若FO=FC，如图2①．
此时点F在△OAB内部，0＜t＜4．
过点A作AH⊥OB于H，延长CF交OB于点T，
由（1）得：CF=CD=
| 6t |
| 5 |
| 4t |
| 5 |
| 3t |
| 5 |
则FT=CT-CF=8-
| 4t |
| 5 |
| 6t |
| 5 |
∵∠FTO=90°，∴FT2+OT2=OF2．
∴（8-2t）2+（6-
| 3t |
| 5 |
| 6t |
| 5 |
整理得：73t2-980t+2500=0．
解得：t1=
| 250 |
| 73 |
∵0＜t＜4，∴t=
| 250 |
| 73 |
②若CO=CF，如图2②．
此时点F在△OAB外部，4＜t＜10．
∵CF=CD=
| 6t |
| 5 |
∴
| 6t |
| 5 |
解得：t=
| 50 |
| 11 |
③若OC=OF，如图2③．
此时点F在△OAB外部，4＜t＜10．
则有CM=8-
| 4t |
| 5 |
| 6t |
| 5 |
∵OC=OF，OM⊥CF，
∴CM=FM=
| 1 |
| 2 |
∴8-
| 4t |
| 5 |
| 1 |
| 2 |
| 6t |
| 5 |
解得：t=
| 40 |
| 7 |
综上所述：当t为
| 250 |
| 73 |
| 50 |
| 11 |
| 40 |
| 7 |
点评：本题考查了相似三角形的判定与性质、正方形的性质、等腰三角形的性质、平行四边形的判定与性质、解一元二次方程、勾股定理等知识，有一定的综合性，而考虑临界位置及分类讨论则是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目