题目内容
关于x的一元二次方程mx2-(3m+1)x+2m+2=0两实数根为x1,x2,且n=x2-x1-1,则在直角坐标系中,动点P(m,n)形成的曲线的解析式为 .
考点:根与系数的关系
专题:计算题
分析:根据根与系数的关系得到x1+x2=
,x1x2=
,再利用完全平方公式可计算出|x2-x1|=|
|,则n=
-1或n=-
-1,所以mn=-1或mn=-2m+1,根据反比例函数上点的坐标特征当mn=-1时,得到动点P(m,n)形成的曲线的解析式为y=-
.
| 3m+1 |
| m |
| 2m+2 |
| m |
| m-1 |
| m |
| m-1 |
| m |
| m-1 |
| m |
| 1 |
| x |
解答:解:根据题意得x1+x2=
,x1x2=
,
|x2-x1|=
=
=|
|,
所以n=
-1或n=-
-1,
所以mn=-1或mn=-2m+1,
当mn=-1时,动点P(m,n)形成的曲线的解析式为y=-
.
故答案为y=-
.
| 3m+1 |
| m |
| 2m+2 |
| m |
|x2-x1|=
| (x1+x2)2-4x1x2 |
(
|
| m-1 |
| m |
所以n=
| m-1 |
| m |
| m-1 |
| m |
所以mn=-1或mn=-2m+1,
当mn=-1时,动点P(m,n)形成的曲线的解析式为y=-
| 1 |
| x |
故答案为y=-
| 1 |
| x |
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
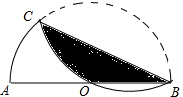 已知半径为6的半圆,沿BC对折,
已知半径为6的半圆,沿BC对折, |
| BC |
| A、6π | ||
B、4
| ||
C、3
| ||
D、2
|
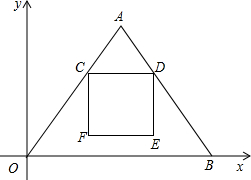 如图,在平面直角坐标系xOy中,等腰△OAB的顶点A在第一象限,底边OB在x轴的正半轴上,且AO=AB=10cm,OB=12cm.动点C从点A出发,沿AO边向O点运动(不与O点重合),速度为1cm/s,运动时间为ts.过点C作CD∥OB交AB于点D.以CD为边,在点A的异侧作正方形CDEF.
如图,在平面直角坐标系xOy中,等腰△OAB的顶点A在第一象限,底边OB在x轴的正半轴上,且AO=AB=10cm,OB=12cm.动点C从点A出发,沿AO边向O点运动(不与O点重合),速度为1cm/s,运动时间为ts.过点C作CD∥OB交AB于点D.以CD为边,在点A的异侧作正方形CDEF. 如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移得到△OBD.连结AD,交OC于点E,求点E坐标.
如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移得到△OBD.连结AD,交OC于点E,求点E坐标.