题目内容
6.在下列条件中①∠A+∠B=∠C②∠A:∠B:∠C=1:2:3③∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C④∠A=∠B=2∠C⑤∠A=∠B=$\frac{1}{2}$∠C中能确定△ABC为直角三角形的条件有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据直角三角形的判定对各个条件进行分析,从而得到答案.
解答 解:①、∵∠A+∠B+∠C=180°,
∴∠A+∠B=∠C=$\frac{1}{2}$×180°=90°,
∴△ABC是直角三角形,故小题正确;
②、∵∠A:∠B:∠C=1:2:3,
∴∠A=30°,∠B=60°,∠C=90°,
∴△ABC是直角三角形,故本小题正确;
③、设∠A=x,∠B=2x,∠C=3x,则x+2x+3x=180°,
解得x=30°,故3x=90°,
∴△ABC是直角三角形,故本小题正确;
④∵设∠C=x,则∠A=∠B=2x,
∴2x+2x+x=180°,解得x=36°,
∴2x=72°,故本小题错误;
⑤∵∠A=∠B=$\frac{1}{2}$∠C,
∴∠A+∠B+∠C=$\frac{1}{2}$∠C+$\frac{1}{2}$∠C+∠C=2∠C=180°,
∴∠C=90°,故本小题正确.
综上所述,是直角三角形的是①②③⑤共4个.
故选C.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
16.化简:
(1)-3x+2y-5x-7y
(2)-5m2n+4mn2-2mn+6m2n+3mn
(3)(4x2y-3xy2)-(1+4x2y-3xy2)
(4)4y2-[3y-(3-2y)+2y2].
(1)-3x+2y-5x-7y
(2)-5m2n+4mn2-2mn+6m2n+3mn
(3)(4x2y-3xy2)-(1+4x2y-3xy2)
(4)4y2-[3y-(3-2y)+2y2].
17.下列语句属于命题的是( )
| A. | 作直线AB的平行线 | B. | 同旁内角相等 | ||
| C. | ∠1与∠2互余吗 | D. | 在线段AB上取点C |
14.在代数式xy2中,x与y的值各减少了$\frac{1}{4}$,则该代数式的值减少了( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{37}{64}$ | D. | $\frac{27}{64}$ |
11.下列说法正确的是( )
| A. | 过一点有且只有一条直线与已知直线垂直 | |
| B. | 直线外一点与直线上各点连接的所有线段中,垂线最短 | |
| C. | 直线外一点到已知直线的垂线段叫做这点到已知直线的距离 | |
| D. | 平行于同一直线的两条直线平行 |
15.一元二次方程x2-10x+21=0的解是( )
| A. | -7 | B. | 3 | C. | 7或3 | D. | -7或3 |
16.如图所示的直角三角形中,m的值为5的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
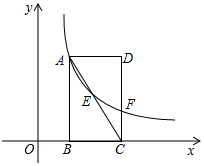 如图直角坐标系中,矩形ABCD的边BC在x轴上,点B、D的坐标分别为B(1,0),D(3,3).
如图直角坐标系中,矩形ABCD的边BC在x轴上,点B、D的坐标分别为B(1,0),D(3,3).