题目内容
9.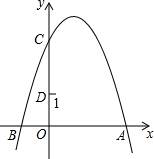 如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).
如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).
分析 当△PCD是以CD为底的等腰三角形时,则P点在线段CD的垂直平分线上,由C、D坐标可求得线段CD中点的坐标,从而可知P点的纵坐标,代入抛物线解析式可求得P点坐标.
解答 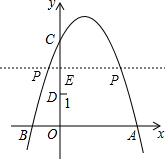 解:
解:
∵△PCD是以CD为底的等腰三角形,
∴点P在线段CD的垂直平分线上,
如图,过P作PE⊥y轴于点E,则E为线段CD的中点,
∵抛物线y=-x2+2x+3与y轴交于点C,
∴C(0,3),且D(0,1),
∴E点坐标为(0,2),
∴P点纵坐标为2,
在y=-x2+2x+3中,令y=2,可得-x2+2x+3=2,解得x=1±$\sqrt{2}$,
∴P点坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2),
故答案为:(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).
点评 本题主要考查等腰三角形的性质,利用等腰三角形的性质求得P点纵坐标是解题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
4. 如图,几何体的俯视图是( )
如图,几何体的俯视图是( )
 如图,几何体的俯视图是( )
如图,几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
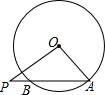 如图,已知⊙O的半径为6cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA的值是$\frac{\sqrt{5}}{3}$.
如图,已知⊙O的半径为6cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA的值是$\frac{\sqrt{5}}{3}$.