题目内容
20.已知x2+mx+25是完全平方式,则m=±10.分析 根据a2±2ab+b2=(a±b)2,x2+mx+25=x2+mx+52,可得m=±2×5=±10,据此解答即可.
解答 解:∵x2+mx+25=x2+mx+52是完全平方式,
∴m=±2×5=±10.
故答案为:±10.
点评 此题主要考查了完全平方式,要熟练掌握,解答此题的关键是要明确计算口诀:首末两项算平方,首末项乘积的2倍中间放,符号随中央.(就是把两项的乘方分别算出来,再算出两项的乘积,再乘以2,然后把这个数放在两数的乘方的中间,这个数以前一个数间的符号随原式中间的符号,完全平方和公式就用+,完全平方差公式就用-,后边的符号都用+);解答此题还要注意m有两个值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列计算正确的是( )
| A. | 3x2-2x2=x2 | B. | x5+x5=x10 | C. | (x5)5=x10 | D. | x20÷x2=x10 |
12.下列运算中,正确的是( )
| A. | a2+a2=a4 | B. | a6÷a2=a4 | C. | (a3)3=a27 | D. | a3•a4=a12 |
9.下列直线表示的不是y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
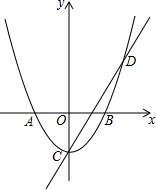 如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.
如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D. 如图,AB∥CD,∠A=32°,∠C=70°,则∠F=38°.
如图,AB∥CD,∠A=32°,∠C=70°,则∠F=38°.