题目内容
 已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.考点:平行四边形的判定,三角形中位线定理
专题:证明题
分析:首先连接BD,根据三角形中位线定理可得HE∥DB,HE=
BD,GF=
DB,FG∥DB,进而得到FG∥HE,GF=HE,然后再根据一组对边平行且相等的四边形是平行四边形得到结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 证明:连接BD,
证明:连接BD,
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴HE∥DB,HE=
BD,GF=
DB,FG∥DB,
∴FG∥HE,GF=HE,
∴四边形EFGH是平行四边形.
 证明:连接BD,
证明:连接BD,∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴HE∥DB,HE=
| 1 |
| 2 |
| 1 |
| 2 |
∴FG∥HE,GF=HE,
∴四边形EFGH是平行四边形.
点评:此题主要考查了三角形中位线定理,以及平行四边形的判定,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
如果把分式
中的a、b都扩大2倍,那么分式的值一定( )
| a |
| a-b |
| A、是原来的2倍 | ||
| B、是原来的4倍 | ||
C、是原来的
| ||
| D、不变 |
当x为任意实数时,下列分式一定有意义的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
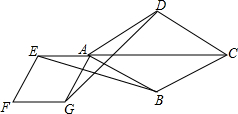 如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD.
如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD.
 如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).
如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).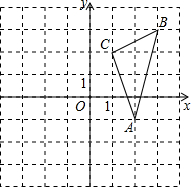 如图,平面直角坐标系中,△ABC的顶点都在网格点上.
如图,平面直角坐标系中,△ABC的顶点都在网格点上.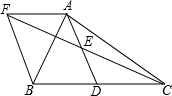 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且BD=DC,连接BF,求证:四边形AFBD为平行四边形.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且BD=DC,连接BF,求证:四边形AFBD为平行四边形.