题目内容
16．抛物线y=-2（x-$\sqrt{2}$）2-2的顶点的坐标是（$\sqrt{2}$，-2）．分析 根据函数y=-2（x-$\sqrt{2}$）2-2，可以直接写出它的顶点坐标，本题得以解决．
解答 解：∵y=-2（x-$\sqrt{2}$）2-2，
∴抛物线y=-2（x-$\sqrt{2}$）2-2的顶点的坐标是（$\sqrt{2}$，-2），
故答案为：（$\sqrt{2}$，-2）．
点评 本题考查二次函数的性质，解题的关键是明确二次函数的性质，由顶点式可以直接写出顶点坐标．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
6．
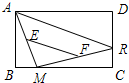如图，矩形ABCD中，点R沿CD边从点C向点D运动，点M在BC边上运动，E、F分别是AM、MR的中点，则EF的长度随着点M、点R的运动（ ）
如图，矩形ABCD中，点R沿CD边从点C向点D运动，点M在BC边上运动，E、F分别是AM、MR的中点，则EF的长度随着点M、点R的运动（ ）| A． | 变短 | B． | 变长 | C． | 不变 | D． | 无法确定 |
7．下列式子：$\frac{3}{a+b}$，4ab，$\frac{{x}^{2}-y}{π}$，$\frac{2xy}{3}$，3-$\frac{3}{b}$中是分式的个数为（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
如图，∠1、∠2、∠3、∠4、∠5．是五边形ABCDE的外角，则∠1+∠2+∠3+∠4+∠5=360°．
1．已知：最简二次根式$\sqrt{5a-1}$与$\sqrt{10a-16}$能合并，则a的值是（ ）
| A． | 2 | B． | -2 | C． | 3 | D． | 4.5 |
在同一平面内如图，EG∥BC，CD交EG于点F，那么图中与∠1相等的角共有2个．
如图，△ABC≌△ADE，BC的延长线交DE于点G，若∠B=24°，∠CAB=54°，∠DAC=16°，则∠DGB=70°．