题目内容
2.(1)计算:($\frac{1}{3}$)-1+$\sqrt{8}$+sin30°;(2)先化简,再求值:(m+2)(m-2)-(m-2)2+1,其中m=2.
分析 (1)原式利用负整数指数幂,二次根式性质,以及特殊角的三角函数值计算即可得到结果;
(2)原式利用平方差公式,以及完全平方公式化简,去括号合并得到最简结果,把m的值代入计算即可求出值.
解答 解:(1)原式=3+2$\sqrt{2}$+$\frac{1}{2}$=3$\frac{1}{2}$+2$\sqrt{2}$;
(2)原式=m2-4-m2+4m-4+1=4m-7,
当m=2时,原式=8-7=1.
点评 此题考查了整式的混合运算-化简求值,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
12.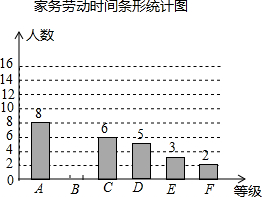 某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分A、B、C、D、E、F六个等级,绘制了如图所示的不完整的统计图表:
某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分A、B、C、D、E、F六个等级,绘制了如图所示的不完整的统计图表:
家务劳动时间统计表
请根据图表中提供的信息,解答下面的问题:
(1)这次一共调査了40位家长,家务劳动时间统计表中的a=16 ,b=5%;
(2)请把家务劳动时间条形统计图补充完整;
(3)若绘制“家务劳动时间扇形统计图”,等级为“D”所对应扇形的圆心角是45度;
(4)若该中学有3000名学生,估计周末家务劳动时间在40分钟以上的学生有1800人.
 某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分A、B、C、D、E、F六个等级,绘制了如图所示的不完整的统计图表:
某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分A、B、C、D、E、F六个等级,绘制了如图所示的不完整的统计图表:家务劳动时间统计表
| 等级 | 家务劳动时间 (分钟) | 人数 | 百分比 |
| A | 50以上 | 8 | 20% |
| B | 41-50 | a | 40% |
| C | 31-40 | 6 | 15% |
| D | 21-30 | 5 | 12.5% |
| E | 11-20 | 3 | 7.5% |
| F | 0-10 | 2 | b |
(1)这次一共调査了40位家长,家务劳动时间统计表中的a=16 ,b=5%;
(2)请把家务劳动时间条形统计图补充完整;
(3)若绘制“家务劳动时间扇形统计图”,等级为“D”所对应扇形的圆心角是45度;
(4)若该中学有3000名学生,估计周末家务劳动时间在40分钟以上的学生有1800人.
14.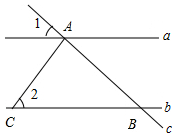 如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=44°,则∠2的度数是( )
如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=44°,则∠2的度数是( )
 如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=44°,则∠2的度数是( )
如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=44°,则∠2的度数是( )| A. | 36° | B. | 44° | C. | 46° | D. | 56° |
11.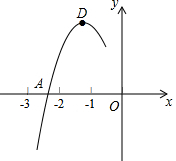 抛物线y=ax2+bx+c的顶点D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c>0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根.
抛物线y=ax2+bx+c的顶点D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c>0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根.
其中正确的结论是( )
 抛物线y=ax2+bx+c的顶点D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c>0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根.
抛物线y=ax2+bx+c的顶点D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c>0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根.其中正确的结论是( )
| A. | ③④ | B. | ②④ | C. | ②③ | D. | ①④ |
12.比-1大1的数是( )
| A. | -2 | B. | 0 | C. | 2 | D. | 3 |
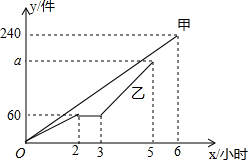 甲、乙两组工人同时开始加工某种零件,乙组在工作2小时后停产1小时更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与开工后时间x(时)之间的函数图象如图1所示.
甲、乙两组工人同时开始加工某种零件,乙组在工作2小时后停产1小时更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与开工后时间x(时)之间的函数图象如图1所示.