题目内容
7.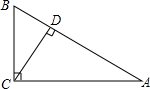 如图,在Rt△ABC中.∠ACB=90°.CD⊥AB于D,若3BC=2AD,求tan∠BCD.
如图,在Rt△ABC中.∠ACB=90°.CD⊥AB于D,若3BC=2AD,求tan∠BCD.
分析 由3BC=2AD,得出$\frac{BC}{AD}$=$\frac{2}{3}$,所以可设BC=2k,则AD=3k,再证明∠BCD=∠A,那么$\frac{BD}{2k}$=$\frac{2k}{BD+3k}$,求出BD=k,然后在Rt△BCD中,利用勾股定理求出CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\sqrt{3}$k,再根据正切函数的定义即可求解.
解答 解:∵3BC=2AD,
∴$\frac{BC}{AD}$=$\frac{2}{3}$,
∴可设BC=2k,则AD=3k,显然k>0.
∵∠ACB=90°,CD⊥AB于D,
∴∠BCD=∠A=90°-∠B,
∴sin∠BCD=sin∠A,
∴$\frac{BD}{2k}$=$\frac{2k}{BD+3k}$,
∴BD2+3kBD-4k2=0,
解得BD=k,或BD=-4k(不合题意舍去).
在Rt△BCD中,∵∠BDC=90°,BC=2k,BD=k,
∴CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\sqrt{3}$k,
∴tan∠BCD=$\frac{BD}{CD}$=$\frac{k}{\sqrt{3}k}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了解直角三角形,比例的性质,锐角三角函数的定义,勾股定理,根据已知条件设BC=2k,再求出BD=k是解题的关键.

练习册系列答案
相关题目
18.位似图形的位似中心可以在( )
| A. | 原图形外 | B. | 原图形内 | C. | 原图形的边上 | D. | 以上三种都可以 |
19.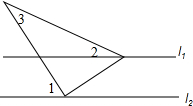 如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )
如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )
 如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )
如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )| A. | 26°40′ | B. | 27°20′ | C. | 27°40′ | D. | 73°20′ |
16.下列各数中最小的是( )
| A. | -5 | B. | -4 | C. | 3 | D. | 4 |
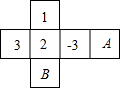 如图,是一个正方体纸盒的展开图,在其中的四个正方形内标有数字1、2、3和-3在其余正方形内分别填上A和B,使得折成正方体后,相对面上的两数互为相反数,则A+B的值是-3.
如图,是一个正方体纸盒的展开图,在其中的四个正方形内标有数字1、2、3和-3在其余正方形内分别填上A和B,使得折成正方体后,相对面上的两数互为相反数,则A+B的值是-3.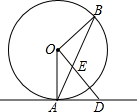 已知:如图,AB是⊙O的弦,OD⊥OB,交AB于点E,且AD=ED.判断直线AD和⊙O的位置关系,并说明理由.
已知:如图,AB是⊙O的弦,OD⊥OB,交AB于点E,且AD=ED.判断直线AD和⊙O的位置关系,并说明理由.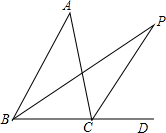 如图,BP,CP分别平分∠ABD,∠ACD,若∠A=40°,求∠P.
如图,BP,CP分别平分∠ABD,∠ACD,若∠A=40°,求∠P.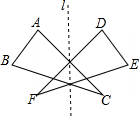 如图,△ABC沿着直线l翻折,与△DEF完全重合,那么我们就说这两个三角形成轴对称.请判断下列说法是否正确.并更正错误的.
如图,△ABC沿着直线l翻折,与△DEF完全重合,那么我们就说这两个三角形成轴对称.请判断下列说法是否正确.并更正错误的.