题目内容
4.若点P是△ABC的∠B,∠C两内角平分线的交点,∠BPC=130°,则∠A的度数是80°.分析 先根据三角形内角和定理求出∠PBC+∠PCB的度数,再根据角平分线的性质求出∠ABC+∠ACB的度数,由三角形内角和定理即可求出答案.
解答 解:∠PBC+∠BCP+∠BPC=180°,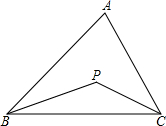
∵∠BPC=130°,
∴∠ABC+∠ACB=100°,
∵BP、CP是角平分线,
∴∠ABC=2∠PBC,∠ACB=2∠BCP,
∴∠ABC+∠ACB=100°,
∵∠ABC+∠ACB+∠A=180°,
∴∠A=80°.
故答案为:80°.
点评 本题考查的是三角形内角和定理及角平分线的性质,注意条件的转换.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
19.355、444、533的大小关系是( )
| A. | 355<444<533 | B. | 444<355<533 | C. | 533<444<355 | D. | 533<355<444 |
13.不等式2x<4的解集为( )
| A. | x<$\frac{1}{2}$ | B. | x<2 | C. | x>$\frac{1}{2}$ | D. | x>2 |
14.已知点A(-1,y1),A(-3,y2)都在反比例函数y=$\frac{k}{x}$(k>0)的图象上,则y1与y2的大小关系为( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法确定 |
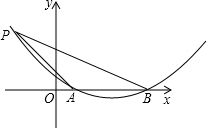 如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,AB=4,P是抛物线上一点,它的横坐标为-2,∠PAO=45°,cot∠PBO=$\frac{7}{3}$,求:
如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,AB=4,P是抛物线上一点,它的横坐标为-2,∠PAO=45°,cot∠PBO=$\frac{7}{3}$,求: 如图,长方形硬纸板以其中任意一边为轴旋转都可得到一个圆柱,你认为以3厘米长的边为轴旋转得到的圆柱体积较大.
如图,长方形硬纸板以其中任意一边为轴旋转都可得到一个圆柱,你认为以3厘米长的边为轴旋转得到的圆柱体积较大.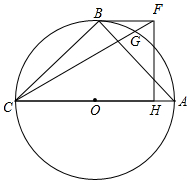 如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.
如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.
 若将三个数$\sqrt{3}$,3$\sqrt{2}$,2$\sqrt{3}$表示在数轴上,则能被如图所示的墨迹覆盖的数是$\sqrt{3}$.
若将三个数$\sqrt{3}$,3$\sqrt{2}$,2$\sqrt{3}$表示在数轴上,则能被如图所示的墨迹覆盖的数是$\sqrt{3}$.