题目内容
9.如图,在△ABD中,AB=AD,将△ABD沿BD翻折,使点A翻折到点C.E是BD上一点,且BE>DE,连结CE并延长交AD于F,连结AE.(1)依题意补全图形;
(2)判断∠DFC与∠BAE的大小关系并加以证明;
(3)若∠BAD=120°,AB=2,取AD的中点G,连结EG,求EA+EG的最小值.
分析 (1)将△ABD沿BD翻折,使点A翻折到点C.E是BD上一点,且BE>DE,连结CE并延长交AD于F,连结AE,据此画图即可;
(2)根据△ABE≌△CBE(SAS),可得∠BAE=∠BCE.再根据AD∥BC,可得∠DFC=∠BCE,进而得出∠DFC=∠BAE;
(3)连接CG,AC,根据EC+EG≥CG可知,CG长就是EA+EG的最小值,根据△ACD为边长为2的等边三角形,G为AD的中点,运用勾股定理即可得出CG=$\sqrt{3}$,进而得到EA+EG的最小值.
解答 解:(1)如图所示: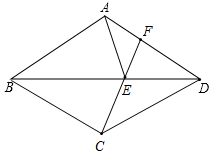
(2)判断:∠DFC=∠BAE.
证明:∵将△ABD沿BD翻折,使点A翻折到点C.
∴BC=BA=DA=CD.
∴四边形ABCD为菱形.
∴∠ABD=∠CBD,AD∥BC.
又∵BE=BE,
∴△ABE≌△CBE(SAS).
∴∠BAE=∠BCE.
∵AD∥BC,
∴∠DFC=∠BCE.
∴∠DFC=∠BAE.
(3)如图,连接CG,AC.
由轴对称的性质可知,EA=EC,
∴EA+EG=EC+EG,
根据EC+EG≥CG可知,CG长就是EA+EG的最小值.
∵∠BAD=120°,四边形ABCD为菱形,
∴∠CAD=60°.
∴△ACD为边长为2的等边三角形.
又∵G为AD的中点,
∴DG=1,
∴Rt△CDG中,由勾股定理可得CG=$\sqrt{3}$,
∴EA+EG的最小值为$\sqrt{3}$.
点评 本题主要考查了折叠问题,菱形的性质以及勾股定理的运用,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
20.下列各式,分解因式正确的是( )
| A. | a2-2ab+b2=(a-b)2 | B. | xy+xz+x=x(y+z) | C. | x2+x3=x3($\frac{1}{x}$+1) | D. | a2+b2=(a+b)2 |
17. 如图,将正方形ABCD逆时针旋转得到正方形AB′C′D′,则旋转角度为( )
如图,将正方形ABCD逆时针旋转得到正方形AB′C′D′,则旋转角度为( )
 如图,将正方形ABCD逆时针旋转得到正方形AB′C′D′,则旋转角度为( )
如图,将正方形ABCD逆时针旋转得到正方形AB′C′D′,则旋转角度为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
14.下列命题中,真命题是( )
| A. | 4的平方根是2 | B. | 同位角相等,两直线平行 | ||
| C. | 同旁内角互补 | D. | 0没有立方根 |
18.某运动鞋生产厂家在街头随机调查男生的鞋号,并得到一组数据,他们最关注这数据中的( )
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
 在正方形ABCO中,A(0,4),B(4,4),C(4,0),O(0,0),E为AO的中点,F为边CO上的动点,分别连接EF,FB,BE得到△EFB,并将其沿FB折叠得到△E′FB.
在正方形ABCO中,A(0,4),B(4,4),C(4,0),O(0,0),E为AO的中点,F为边CO上的动点,分别连接EF,FB,BE得到△EFB,并将其沿FB折叠得到△E′FB.