题目内容
17.计算(1)(-2.48)+(+4.33)+(-7.52)+(-4.33)
(2)(+3$\frac{5}{6}$)+(-5$\frac{1}{7}$)+(-2$\frac{1}{6}$)+(-32$\frac{6}{7}$)
(3)$\frac{4}{5}$-(+$\frac{5}{6}$)-(+$\frac{3}{5}$)+$\frac{1}{6}$
(4)-14-$\frac{1}{6}$×[2-(-3)2].
分析 (1)原式结合后,相加即可得到结果;
(2)原式结合后,相加即可得到结果;
(3)原式结合后,相加即可得到结果;
(4)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果.
解答 解:(1)原式=(-2.48-7.52)+[(+4.33)+(-4.33)]=-10;
(2)原式=(3$\frac{5}{6}$-2$\frac{1}{6}$)+(-5$\frac{1}{7}$-32$\frac{6}{7}$)=1$\frac{2}{3}$-38=-36$\frac{1}{3}$;
(3)原式=($\frac{4}{5}$-$\frac{3}{5}$)+(-$\frac{5}{6}$+$\frac{1}{6}$)=$\frac{1}{5}$-$\frac{2}{3}$=-$\frac{7}{15}$;
(4)原式=-1-$\frac{1}{6}$×(2-9)=-1-$\frac{1}{6}$×(-7)=-1+$\frac{7}{6}$=$\frac{1}{6}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.如果$\sqrt{{a}^{2}}$-a=b成立,且b>0,则a取值范围是( )
| A. | a<0 | B. | a>0 | C. | a≥0 | D. | 无法确定 |
6.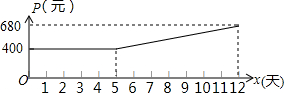 某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.
某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.
(1)求药品每天的产量y(吨)是时间x(天)之间的函数关系式;
(2)当5≤x≤12时,直接写出P(元)与时间x(天)的函数关系是P=P=40x+200;
(3)若这批药品的价格为1400元/吨,每天的利润设为W元,求哪一天的利润最高,最高利润是多少?(利润=价格-成本)
(4)为了提高工人加班的津贴,药厂决定在(3)中价格的基础上每吨药品加价a元,但必须满足从第5天到第12天期间,每吨加价a后每天的利润随时间的增大而增大,直线写出a的最小值.
 某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.
某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.| 时间x(天) | 2 | 4 |
| 每天产量y(吨) | 24 | 28 |
(2)当5≤x≤12时,直接写出P(元)与时间x(天)的函数关系是P=P=40x+200;
(3)若这批药品的价格为1400元/吨,每天的利润设为W元,求哪一天的利润最高,最高利润是多少?(利润=价格-成本)
(4)为了提高工人加班的津贴,药厂决定在(3)中价格的基础上每吨药品加价a元,但必须满足从第5天到第12天期间,每吨加价a后每天的利润随时间的增大而增大,直线写出a的最小值.

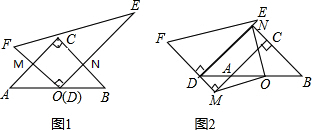
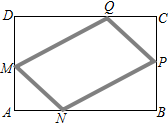 在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=x m,已知矩形的边BC=200m,边AB=a m,a为大于200的常数,设四边形MNPQ的面积为sm2
在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=x m,已知矩形的边BC=200m,边AB=a m,a为大于200的常数,设四边形MNPQ的面积为sm2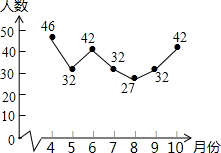 在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )
在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )